THE STRINGENT LIMITATIONS IMPOSED BY TRIGONOMETRY.

Those who laboured so long and so diligently to build the Great Pyramid did not undertake to build a "ruined" structure. The fact that the Great Pyramid falls, officially, 2 inches short of 756 British Standard feet in its base length can be attributed to thousands of years of neglect, wear, tear, human parasites, earthquakes and general deterioration of the exposed structure in a reasonably hostile environment.
Its intended, original design specifications called for finished, pristine dimensions of 756 feet per base side, such that multiple, interrelating codes could exist within that versatile base-side value.

To the multi-use base measurement was added a dynamic angle code of 51.84-degrees, which was integral to the geodetic systems or to the number values describing the duration of the Precession of the Equinoxes.

A range of mathematical checks and balances and obligatory codes, stopped the pyramid short of achieving a pointed apex. The design specifications called for an altar at a vertical height of exactly 453.049492 feet (280 PHI feet or 168 Megalithic Yards). The height was of great importance, as it had to equate, by varied, marginally different assignments, to the "ring of the Earth", ratio measurements.

The face diagonal value was intended to code, specifically, 576 feet, but with so many codes to incorporate 3 dimensionally, a small compromise was required and there was an allowable overrun of 2 1/2 inches (576.1874059 feet overall).

By the three dimensional convergence of trigonometrically limiting factors onto the top section of the pyramid, vertically, diagonally and horizontally (by diminishing PHI factors), there was no leeway or choice in what the final upper dimensions could be. The top section was locked into resolving to a square, flat floor width of 44 feet diameter (43.9941463 feet actual).

There are astronomical and navigational numbers, which recur on standing stone circle sites or important community shared structures around the world. These codes provide us with strong clues regarding what should be found on the Great Pyramid, inasmuch as evidence would suggest it was the main source and primary repository of mathematical codes, used for the establishment of worldwide colonies. Outlying peoples would need these mathematical gems of civilisation in order to maintain organised, functional societies.

Because of three such codes, 51.84, 11.52 & 45, it was obligatory that there be a terrace, ringing the altar atop the Great Pyramid and set to an exact height of 450 feet...51.84 ÷ 11.52 = 4.5...or 5184 ÷ 11.52 = 450. A terrace would have been incorporated into the design at this exact point because of the need for the vertical walls of the altar to contain square footage area codes related to the mile geodetic increment (44 feet X 3 feet X 4 faces = 528 square feet...the British Standard mile was 5280 feet).

The pyramid's sub-structure was built as 201 tiers of stacked blocks, with the 201st tier being the altar. This means that the tier "average", excluding the specialised altar section, was 2.25 feet (11/2 Celtic common cubits) per stepped tier. The casing stones would have stopped at the 450 feet terrace height, affording the astronomer/ mathematicians a ledge of 28 inches width (28.75521811 inches actual), from which they could work. This circumnavigating terrace width, although not overly generous, was sufficient to provide an adequate working environment, as well as a protective fence, slightly under 3 feet of height, to ensure safe containment of working personnel.

The overall length of the terrace, edge to edge, would have been 48.79253635 feet, but would have coded 48 feet inward of the fence line. The symbolic height of the pyramid, based upon where diagonal face lines, running up from the base, would nave converged above the centre of the altar floor, was 480 feet. Trigonometry dictates that the vertical height to this point would have, in actuality, been closer to 481 feet.

It's also possible that a skirt ramp existed at the terrace level, which jutted beyond the casing stone face line and incorporated a stairwell down to an entry door leading inside the pyramid. Plain and basic common sense tells us that the Priests went to their workstations via internal corridors and stair systems.

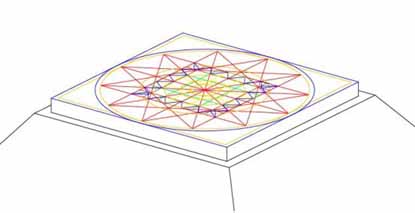
Figure 8: It is the author's opinion that the top section of the Great Pyramid would have looked very much like this and would have incorporated, at least, this much of the universal astronomical geometry atop its "plane table" altar floor. From this elevated position above the Giza Plateau, all four quarters of the Earth could be viewed simultaneously, with no obstruction to the view except, possibly, the marginally higher point of Khafre Pyramid (coded to be 19.5 feet higher, vertically, than the Great Pyramid @ 472.5 feet...the 19.5 number relates to the Sabbatical calendar system). It's probable that annual fixes were taken on stars alighting onto the Khafre Pyramid's pinnacle and it acted as an outer marker, of specific known degree angle, to the Great Pyramid's altar. The Giza Plateau, itself, is inclined and the possibility is that the altar of the Great Pyramid was the loftiest, pre-eminent position.

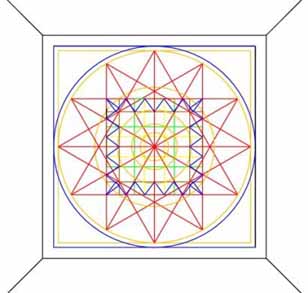
Figure 9: The altar would have displayed at least this much of the star, cross and PHI related geometry, as well as the geodetic ring calibrations. When one considers the geometrically perfect but stark bare walls of the inner pyramid, it would seem that these ancient people did not embellish anything unnecessarily. They appear to have avoided the ostentatious in preference to the sophisticated but functional. The builders of the Great Pyramid and associated structures were not the Dynastic Egyptians, but predated them by millenniums. The late era residents of the region embellished everything with their colourful symbols and hieroglyphics...none of which displayed any aspect of building these magnificent edifices. The chessboard matrix is an abbreviation of layered geometry and infers considerably more than is here shown. It can, accordingly, be expanded at will, as the chessboard provides the base intersections for the fuller geometry. Given that there is no real leeway in the dimensions or opportunity, thereby, to introduce a range of customised functions, what was happening on this altar?

1. The dimensions of the altar are 44 feet X 44 feet. That equates to 8 fathoms per side or 64 sq. fathoms. The sum of 8 fathoms is 1/375th of an ancient league (3.125 miles).

2. The inch value of 1 side was 528, in recognition of the mile at 5280 feet.

3. The perimeter value was 176 feet, in recognition of the 1760 yards in a mile.

4. The square footage value for the vertical walls was 132 feet per side or 528 for all 4 faces. The Menkaure Pyramid, under its PHI assignment, was 132 megalithic yards (32.360678 inches per MY) long per side at its base. This PHI length was twice the diameter of "Y" Holes Circle at Stonehenge.

5. The 44 feet diameter circle, extending to the edges of the altar, has a circumference of, essentially, 138.24 feet, using the geodetic rendition of PI @ 3.141818182. A normal PI rendition is very close to this value @ 138.2304 feet. It's probable that the circle was set to a perfect 138.24 feet of circumference value, as this is a fully sexagesimal calibration and is 1/375th of the circumference value of a circle of 1 league diameter.

6. A degree of arc on this circle would be 4.608 inches, which might not appear too dynamic until it is realised that this is 1.152 X 4. Stonehenge's Sarsen Circle's outer rim was 345.6 feet, which was 11.52 inches per degree of arc. A ratio of 1:2.5 exists between the pyramid's altar circle and the Sarsen Circle outer rim. This comparison demonstrates the ancient use of expressions of 11.52 as 1/360th segmentations of a circle.

7. The altar's138.24 feet of circumference is, simply, 11.52 feet X 12, or the distance between ray points of the zodiac star. The distance between the hubstones of the Waitapu standing stone circle in New Zealand is 96 feet or 1152 inches.

8. The inch values of both the pyramid altar circle and the Sarsen Circle are divisible by 51.84, rendering (32...altar) and (80...Sarsen).

9. The foot values of both the pyramid altar and Stonehenge's Sarsen Circle are divisible by 1.728 feet, rendering (80...altar) and (200...Sarsen).

This 44 feet diameter altar circle was undoubtedly used for teaching principles of ancient navigation. The method used an 11 series increment of linear distance covered, which converted exactly into a sexagesimal circumference. This brilliant method allowed for accurate reading of compass angles.
Amon-RA statuettes or the hypocephalus funerary amulet also provide clues that the 12-pointed zodiac star was left in place, whereas the other star, cross or PHI vectors were abbreviated.
It's altogether probable that the very centre of the floor had a drilled, small diameter hole into which a locating dowel for an alidade-sighting rule could be inserted. The alidade would have extended across the entirety of the plane table to provide readings on the altar's dual calibration rings.

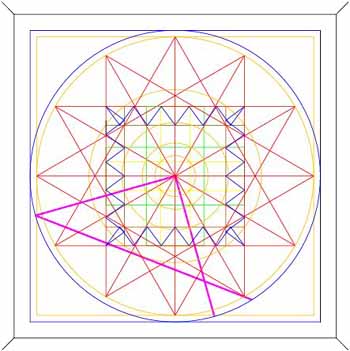
Figure 10: This picture features a specialised 3,4,5 triangle (magenta-purple) that could be swivelled through 360 degrees of arc while fixed to site centre on the intersection of opposite and adjacent. Note the extended vectors of the hypotenuse and adjacent, which reach to the calibrated rim. This kind of swivelling 3,4,5 was used extensively at Stonehenge and also Mt. Pleasant observatory near Dorchester, Dorset, England, where the post-positions acted as locating stations. At the British sites, a series of 3 ropes were used between stations, with the intersection point of opposite and hypotenuse resolving onto the circumnavigating embankment. Evidence at Stonehenge would suggest that the primary usage of the 3,4,5's was related to determining the exact azimuth angles of stars near the horizon. At both Stonehenge and Mt. Pleasant there were many fixed, different 3,4,5 choices through 360 degrees of arc. Star alighting positions, as viewed from a specific central position, were marked on the embankment with a stone and their angles later calculated by trigonometry. In the above picture, note how the line of the swivelling 3,4,5's hypotenuse brushes the overlaying PHI circle of the 64 square chessboard matrix.

The 64 square matrix is 21 feet in diameter and this value was determined by dividing the 42 feet square by PHI, then the resultant value by 1/2 PHI. The second inward circle has a diameter of 42 feet (4 reeds) and is housed within the confines of a 42 feet square. This diameter was 1/18th of the base length of the pyramid and the area of this square was 1/324th of the area of the base. The number 324 was of manifold importance to the ancient system and the "rounded" megalithic yard (32.4 inches) or PHI inch (1.62 inches) were expressions of 324.

The number is also related to the Precessional number...25920 ÷ 324 = 80. The sexagesimal height of the Great Pyramid at 453.6 feet was 168 rounded megalithic yards of 32.4 inches each. The British system of weights is based on dividing pyramid foot measures by 1.62 and 3.24.

Just as an "11 series" length will convert to a sexagesimal circumference, so also can selected sexagesimal lengths convert to an 11 series circumference by a minor manipulation of PI. A diameter of 42 feet, which is sexagesimal/ septimal (6X7), converts smoothly to a circumference of 132 feet (131.9472 feet...about 1/2 an inch short in 132 feet).

A close proximity expression of PI (22 ÷ 7 = 3.142857143) can convert progressions of 7 or sexagesimal/ septimal numbers like 21 & 42 into perfect "11 series" geodetic, "ring of the Earth" numbers.

It appears obvious that this circle was sized to exactly 132 feet of circumference (42.01680672 feet true diameter...enlarged 1/10th of an inch in overall diameter). Remember, the altar sides (44 feet X 3 feet accentuated a code alluding to 132). This is how the circle worked:

1. The ancient "ring of the Earth", under the 11 series assignment, was 7920 leagues. The true, relative equatorial diameter of the Earth is 7920 miles and for ease of calculation, under the "11 series", the size of the league was set to 3.125 miles. The oblate spheroid Earth needed to be treated as a perfect sphere for navigation or grid referencing and a known amount of marginal error had to remain within the reducible system. The ancient "11 series" system fell about 152 miles short on equatorial circumference and about 132 miles short on polar circumference. These shortfalls were so small, in a global sense, as to have no conceivable effect on getting to a destination, especially a regional one. Ocean traversal, without the benefit of satellite navigational references or radio directional beacons, was fraught with difficulty at the best of times and the navigators needed to be aware of all contributing factors to position, 24 hours a day.

2. The 132 feet of circumference would have been reduced to inches, equating to 1584. Each inch would have been divided up into 5 parts equating to 7920 segments overall within the 132 feet. Each 1/5th of an inch would represent a league of 16500 feet or 3.125 miles.

3. Every 4.4 inches would represent 1 degree of arc or 22 leagues (68.75 miles).

4. It would appear that the best way of calibrating this circle was in 1/10th of an inch increments.

5. The distance between ray points of the 12-pointed star was 11 feet or 132 inches.

6. The distance between ray-points represented 660 leagues, 2062.5 miles (remember there was a Dynastic Egyptian Royal Cubit of 20.625 inches), 16500 furlongs, 165000 chains, 660000 rods/ perches, 1980000 fathoms or 16500000 links.

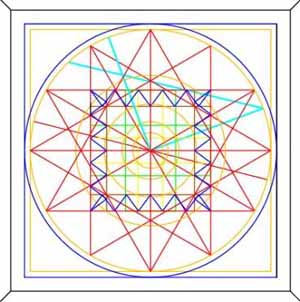
Figure 11: A 3,4,5 triangle (light blue- cyan), sized to the dimensions of the 132 feet circumference circle, is here shown. This 3,4,5 triangle is exactly 1/8th the size of a swirling triangle in use at Stonehenge. That one was 126 feet (adjacent), 168 feet (opposite) and 210 (hypotenuse) and, like this one was based upon the numbers 21 or, more specifically, 42. It is beyond question that such 3,4,5's were in use on the British sites, which lends credence to the fact that they were used on the calibration rings of the pyramid's altar.

Besides the obvious preoccupation of remembering the size of the Earth in 3 geodetic systems and maintaining a high level of expertise in training navigators to guide ships to far-flung destinations, there was also the astronomy.
A large and very important aspect of navigational training related to knowledge of "zenith" stars and the latitudes they would traverse during given months. It was known that varied countries were situated directly under particular stars at specific times of the year and the shipboard, stellar angles to zenith stars provided a crosscheck to the manual plotting undertaken by the navigators.
After gales and turbulent seas had caused disorientation and an inevitable degree of inaccuracy in the estimated position of the ship, the stars helped to re-establish the correct bearing to the destination.
The 64 square, abbreviated matrix atop the pyramid contained the standard knowledge of how fix onto and plot stellar positions with considerable accuracy.
Training for the navigators would have included the reading of shadows cast by poles of known height. Even at sea, if conditions were calm enough, a shadow pole device could still give an accurate reading of the highest position, in the midday sky, reached by the sun. A properly fashioned, compact and transportable shadow pole device would indicate the latitude with excellent relative accuracy.

Figure 12: Picture by G. Fouillé of a Phoenician Roundship (circa 700-1300 BC). These sturdy workboats and cargo vessels were plying the trade routes of the world in the two millenniums preceding the Christian era and were linked to a strong maritime tradition that was many thousands of years older. A fleet of buried ships, found at Abydos, Egypt, were estimated to be 5000 years old. They were assessed by Cheryl Haldane, a nautical archaeologist at Texas A & M University as, 'an advanced design, capable of riding out the most powerful waves and the worst weather of the open seas'.

CONTINUE