THE CASING STONE CODES OF THE GREAT PYRAMID

Sir William Flinders Petrie traveled to Egypt in early 1880 and spent most of that year doing a very comprehensive survey of the pyramids of the Gizeh Plateau. His very careful measurements on the Great Pyramid, as well as those undertaken on the Khafre and Menkaure pyramids, remain the definitive work or authority on this subject. His findings were later published in The Pyramids And Temples Of Gizeh, by W. M. Flinders Petrie, 1883.
To see Petrie's book online CLICK HERE.

As a part of his exhaustive work, Petrie measured the heights of each of the 203 tiers of the Great Pyramid. Because the former, smooth outer casing stones were almost totally stripped away and used for other building purposes centuries ago, the core or backing blocks are nowadays exposed. Researchers like Petrie could, therefore, climb the pyramid step by step to the top and, with the use of a theodolite, take very exacting measurements of rise for each overall tier. Petrie's method was to measure all the way up one side of the pyramid, then all the way down the opposite side.
To see Petrie's results for each core block tier's measured height, CLICK HERE.

Whereas one might expect that each core block tier would rise at a regular, standard height every time, this is not the case. It becomes very evident that the original design intention was for each tier to be different and any individual tier can vary from as little as 20" of rise to as much as 59".

Another point of interest relates to the tier heights being quite abstract values. Although the general measurements and angles used in the construction of the Great Pyramid are recognisable as standards that were used by many other cousin civilisations, the tier rise heights mostly defy recognition. So, why is this?

THE ODD TIER HEIGHTS

Because it was built as a Bureau of Standards edifice, the Great Pyramid was very carefully designed to incorporate important geometric principles in all of its external features. The slope angle was set to 51.84-degrees and the base length to 756-feet. Designed as a truncated pyramid with a level, top altar floor 44' square*, there was also a vertical height code that had to be achieved with considerable accuracy. The only way to maintain the required precision was to have very recognisable lengths coming up the sloping diagonal face, casing stone by casing stone. By using trigonometry and staying abreast of both casing stone face & core block tier rise heights, it could be determined when the correct distance up the face had been achieved, station by station.

Maintaining accuracy in the outer face, upwards diagonal lengths was in direct consequence to getting the tier heights correct. Later, by adding up all the casing stone face value lengths together, it could be known how well the building was progressing. Fortunately, one course of casing stones has survived by being buried deep in sand at the Great Pyramid's base and they tell us a lot about the design features of the casing stones on other levels up the pyramid.

BUT WHY DOES EVERY TIER VARY IN HEIGHT TO SUCH A DEGREE?

The answer appears to be adequately provided by Prof. Joseph Davidovits, discoverer of the fact that the outer casing stones and the core blocks behind them were made of ancient concrete:

'Before the first pyramid built out of stone, the ancient Egyptians constructed very imposing crude brick monuments. We find large funerary temple enclosures of the second dynasty, like the Khasekhemwy one (2,730 B.C.). Its massive wall is of crude clay bricks, therefore in a moulded material. It is generally agreed, since these bricks were worked in moulds, that their dimension must be uniform. However, this is wrong. Despite having been manufactured in moulds, the clay bricks are of approximately 5 different sizes, implying the use of several patterns. We find these differences in proportions in all pyramids. This heterogeneity gives the monuments the ability to resist earthquakes by avoiding the amplification of seismic waves.' See: Why the pharaohs built the Pyramids with fake stones, Joseph Davidovits, Geopolymer Institute, ISBN 9782951482043. http://www.geopolymer.org/fichiers_pdf/pyramid_chapt1.pdf

The bottom course of the Great Pyramid was the highest of any single tier. The measured length up the outer sloping face of the base course casing stones was 75", whereas the rear vertical height achieved almost 59". Because of some meandering in the face line of the rear core blocks that the casing stones sat against, there were variations in the front-to-rear lengths of the casing stones. These variations at the rear didn't matter, as the very precisely made casing stones, as well as the somewhat rougher core blocks immediately behind, were all made of ancient concrete that had been formed up and poured in place. Behind the core blocks were rougher, hewn stones from the quarries and aggregate infill of chipped quarry stones.
For more comprehensive information on this ancient concrete that sets like very hard, high quality limestone rock, CLICK HERE.

The above stone had a measured length of 81" along the face. This would give a square inch value of 6075" (a strong lunar code).

Based upon a scaled topographical drawing of 5 stones (including this one seen with the Egyptian guide standing at its end) provided in Great Pyramid in Fact and Theory, the lengths of adjacent stones were probably 56", 57.6", 88"& 52.5" respectively.

These lengths would have provided square inch codes of 56" .... 4200 sq"(strong navigational & lunar coding); 57.6" .... 4320 sq" (navigational); 88" .... 6600 sq" (navigation using the 5280' mile; 52.5" .... 3937.5 sq" (strong navigational & lunar coding).

Despite the apparent fine, blending finish of the casing stones and their uniform face height per tier, we can confidently surmise that each was sized differently in terms of its length, compared to its immediate neighbors. It is apparent that nothing was arbitrary and that the face dimensions of virtually every casing stone contained a tutorial in terms of the face length, height and square inch values produced.

BACK ENGINEERING THE CASING STONE FACE DIAGONAL LENGTHS UP THE PYRAMID TIER BY TIER.

There are, as stated, 203 tiers that were measured by Petrie and of these the top two were only partially complete, but sufficiently so to know their intended or design heights. In all recorded history the Great Pyramid has never been observed to have a pointed top. It is very evident that this particular pyramid was designed to be truncated and have an altar or observatory platform at its top. In terms of mathematical coding, the height value provided by the 203rd tier (453.6') is quite perfect for a tutorial in navigation that related to the equatorial circumference of the Earth.

According to the careful measurements provided by Petrie, the sparse and jumbled 203rd (top) course achieved a height of 5451.8", which is less that an inch over 453.6'. There were at least 3 close proximity values (two mnemonic and one literal) that the ancient mathematicians would have wanted to be read into the finished height (depending upon which navigational system one was using and calculating by). The values are 453.6', 453.75' & 456.192' (456²⁴/125ths).

THIRTY FIVE COURSES.

Over a series of articles, let's proceed up the pyramid at a rate of 7-courses at a time to the 35th tier.

Tier number 35 was almost twice as high as the course that preceded it and apparently represented a major stage where everything was perfected before commencing the next run. Setting aside the thirty-fifth tier to accomplish this purpose was in keeping with the lunisolar Sabbatical Calendar system and practices, which worked according to the number seven (note: 35 is 70 ÷ 2 or 7 X 5). Under the Sabbatical system, at the end of the seventh or Sabbatical year everything was perfected and corrected before commencing another 7-year calendar cycle. We might yet discover that there will be multiples of these "milestone" points up the pyramid and that each has a relationship to the number seven. Let's now commence the process of back engineering 35 casing stones to see if we can work out the intended face diagonal length for each, based upon the tier measurements provided by Petrie. For many reasons related to ancient mathematical and science-coding systems it's quite obvious that the intended design angle of the Great Pyramid was 51.84-degrees (51° 50' 24"). Petrie's multiple calculations to determine the intended slope angle on the very weather worn edifice hovered close to this highly factorable value and in his summary he stated' On the whole, we probably cannot do better than take 51º 52' ± 2' as the nearest approximation to the mean angle of the Pyramid, allowing some weight to the South side.

Let's look at the first seven courses:

1. Petrie determined that this base tier was 58.6" high on the NE, but 57.6" high on the SW, a difference of an inch across the base expanse of approximately 13 acres.

A number of outer casing blocks survived under the sand at this level and their diagonal face lengths upwards were measured to be 75".

Based upon years of building experience, this researcher assumes that one would wish to have the casing blocks sit either level or slightly proud (higher) than the core blocks behind them. The back-engineering formula related to the vertical height of this base set of casing stones is 75" X 51.84° sin = 58.972" (58²⁴³/250ths).

This means that the perfectly level outer casing blocks would sit about ¹/3rd of an inch proud of the rear core blocks on the NE side, tapering upwards to 1¹/3rd inches higher on the SW. This slight discrepancy in the perimeter level could be rectified by laying down a concrete mortar mix flowing over into irregular low troughs of the core block top surfaces, then leveling everything to perfection before the next course commenced. As any builder knows, it is essential to start off on a foundation that is perfectly level and square or one will encounter problems at each building stage, all the way up to the roof. As it turns out it took the Great Pyramid builders a few courses of adjustments to finally achieve something close to perfection on the 4th course.

Based upon Petrie's drawing of the core blocks for each tier and how the casing stones would have interacted with them, a side-on view of a typical base, outer-casing stone should have looked like this:

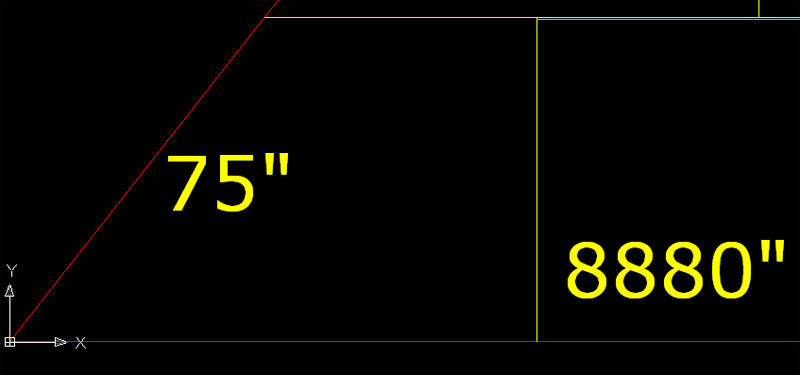
The face diagonal length is 75". Ideally, the base length to the core backing blocks was 96", but this would vary according to irregularities in the face of the core block behind. The rear height was 58.972" and the top of the block was just under 50" long, which again could vary according to how the face of the core block behind sat. Inasmuch as the rear core blocks and the casing stones themselves were concrete that had been formed, poured and hard tamped in place, small irregularities in the core backing didn't matter as all crevices, pockets or fissures were filled, then left to hardened to perfection. A distance of 8880" (740') extended between the back edges of the casing stones on each side of the site and the builders would have poured the core blocks to sit within a perimeter of 740' square.

A thin blue line is seen to undercut the yellow line that indicates the top of the casing stone course. This represents the measured height of the core blocks that sat behind the casing stones. All lines are completed in AutoCAD according to Petrie's recorded heights of the core block tiers.

2. Petrie determined that this tier was 49.1" high on the NE side and 52.5" high on the SW side.

Now the builders have tried to reverse the slight mistake of the first tier, which was out of level by 1" and inclined towards the SW, but they over compensated.

The 2nd casing stone skirt around the pyramid has a face slope length of 65". The formula used was 65" X 51.84° sin = 51.10875". On the SW side of the pyramid the top of the casing stone sits almost perfectly level with the core block behind (the core is ¹/42nd of an inch proud). On the NE side, however, the casing stone top sits almost 2.4 inches proud of the core block behind and there will need to be mortar infill to establish a perfect level over the core block top. The distance up the face of the casing stones has now achieved 140". The core blocks of this second tier sit within a square perimeter of 8800" (733.3333').

3. Petrie determined that this 3rd tier rose 48.2" on the NE side and 45.3" on the SW side.

Again the builders appear to be trying to rectify an overall level that favors the SW side on the tier below. They make the outer diagonal face of the casing blocks for this tier 60" long. The effect now is that the casing stone top sits just over half an inch proud of the core blocks on the NE side and an inch proud on the SW side. The overall distance up the casing stone faces has now achieved 200" and everything is almost perfectly level across the expanse of this tier. The core blocks for this tier sit within a perimeter 8700" square (725').

4. Petrie determined that this 4th tier rose 44" on the NE side and 44.5" on the SW side.

In order to adjust out the last of the error (¹/2" favoring the NE side), the builders make the SW side ¹/2" higher. The result over the entire tier is relative perfection in the level, with the SW side being ¹/69th of an inch higher. The builders form up and pour the casing stones so that the outer faces are 56" long and now the casing stones sit slightly over ¹/2 an inch proud of the core blocks behind. The diagonal length up the casing stones has now grown to 256". The tier rise formula was 56" X 51.84° sin = 44.03125". The 4th tier sits within a perimeter of 8640" square (720').

5. Petrie determined that this 5th tier rose 40.2" on the NE side and 38.9" on the SW side. After having achieved virtual perfection in the level of the 4th tier, the NE side now sits a little over an inch higher than the SW side.

It appears plausible to assume that the diagonal face length of this set of casing stones was 50". The formula was: 50" X 51.84° sin = 39.3144" (intended vertical rise for the core blocks and infill blocks / aggregates behind them).

This would mean that the core blocks on the extreme NE would sit just over ¹/4th of an inch proud of the casing stones there, but this excess would quickly diminish further towards the SW, where the casing stone tops finally sat 1" above the core blocks.

The core blocks for this tier sat within a perimeter of 8580" square (715').

6. Petrie determined that this 6th tier rose 38" on the NE side and 39.6" on the SW side.

Again an attempt is being made to bring everything back into level by favoring the SW side. It would appear that the builders made the casing stone face length 49.5" for this tier. The formula was 49.5" X 51.84° sin = 38.92123" (core block or tier rise).

The core blocks for this tier sat within a perimeter of 8520" square (710').

The diagonal face length has now achieved 355.5".

7. Petrie determined that this 7th tier rose 39.2" on the NE side and 44.1" on the SW side.

Now things are getting seriously out of level internally once again and it will take some extensive remedial work to re-establish perfection. To reset the internal working level for the core blocks and infill materials that they form a perimeter around, the face diagonal length of the casing stones needs to be 56". The formula was: 56" X 51.84° sin = 44.032". This means that the top of the casing stone to the extreme NE side sat an incredible 5.47" higher than the inwards core block and that the core block to the SW side sat ¹/15th of an inch proud of the casing stone top.

The core blocks sat within a perimeter of 8460" square (705').

The diagonal face length has now achieved 411.5".

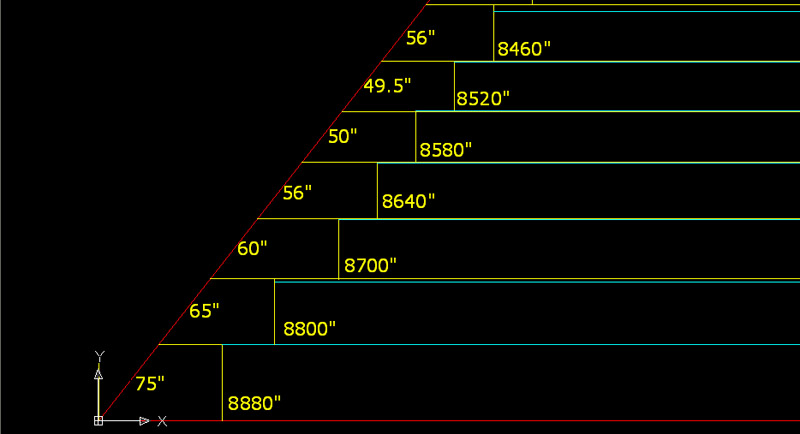
The first seven courses or tiers are shown in the above picture. The slightly out of level blue lines running from one side of the pyramid to the other show the level height of the more inwards core blocks, as measured by Petrie, tier by tier. By this laborious back-engineering exercise in AutoCAD, the reason for the very abstract vertical rise values of the core blocks becomes clear. The only important consideration for the architects was the visibly apparent, finished diagonal face length up the casing stones, which had to equate to a code-bearing number. It can be safely assumed that the pyramid designers-architects would not have wanted to use any complex fractions on this outer face, but would have limited any use of fractions of an inch to values no less that half an inch. To do otherwise would have dramatically increased the risk of error creeping in to the otherwise "optician-like" precision requirements of the casing stone dimensions.

If the ancient scientists were capable of combining specialised (flexible) materials, such that some equivalent to a modern-day hose could be fabricated, then very precise level-elevations could be achieved, tier by tier on all the casing stone tops around the entire pyramid (by use of a simple "water-level" device). We know that they could produce copper pipes. In the absence of a theodolite for shooting levels, a modern-day carpenter, setting out the foundations of a home, can achieve perfect levels all around with nothing more than a water filled garden hose.

And so we've made a start. Some critics might consider this undertaking to be too tedious and futile an exercise to have any merit. However, about 130-yrs ago Petrie took the immense personal trouble to clamber up one side of the Great Pyramid and down the other, taking very precise double-measurements with his theodolite on each tier. He's left us with a grand body of traditionally neglected, albeit painstakingly acquired, information worthy of in-depth analysis. If we are ever to understand the original architectural-design, dimension-intention for consecutive layers of casing stones, then we must do the trigonometry on the core block rises in order to formulate a rational theory.

Martin Doutré

September 2009.

To be continued