The star and cross pattern geometry, in combination with PHI circles and PHI squares, Holy Rectangles, as well as the 7 & 14-pointed stars, constituted the foundation template from which most large observatories were built in many widespread quarters of the ancient world. Because of the tremendous importance placed upon retaining the special knowledge, it was often encoded into the dimensions and angles of ancient "communal" or village structures as well, for ongoing mnemonic reference. An example of this coding is clearly demonstrated in the dimensions of the former Crosshouse of Miringa te Kakara, central North Island, New Zealand, which survived until 1983, when it was destroyed by fire. The ground plan of the Crosshouse at Miringa te Kakara is now used to show how the building complied with the age-old astronomical mathematical formulas found coded into major astronomical sites around the world.

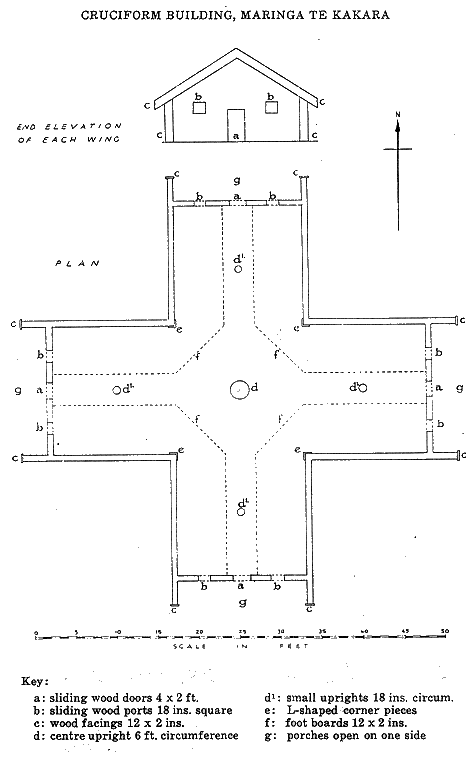
Figure 16: An official ground plan of the Crosshouse of Miringa te Kakara, drawn by architect P. G Hunt in 1958 after a survey of the building. The old structure was being assessed pending restoration. The origins of the building are sketchy, with some historians believing it was built in 1860 by the Maori "Hau Hau" movement. Other researchers cite evidence of a much earlier pre-colonial origin, claiming that the building had existed for many centuries and was only "restored" by followers of the Hau Hau faith. The Maori Hau Hau adherents wished to "bring back" the supernatural, former civilisation called Patu-paiarehe, to combat those working Makutu (witchcraft). The practioners of Makutu were causing many deaths and the restoration of the Crosshouse was seen as a way of enticing the Patu-paiarehe of Rangitoto (mountain range) to remain in their old haunts as guardians to the Ngati- Maniapoto (Maori) people (see, Journal of the Polynesian Society, vol. 30, pg. 146; article by James Cowan).
The followers of the Hau Hau religion adhered to a policy of never changing any aspect of the building, with all defective pieces of structure replaced only after carefully removal and precise copying of the item. The Maori overseers appear to have known that the building contained long forgotten codes, attributable to the Pre-Polynesian Patu-paiarehe people, a fair-skinned civilisation that had initially lived peaceably with the newly arrived Polynesian migrants and who had taught Maori many ancient, Northern European and Mediterranean cultural expressions. At a later era fierce warriors cannibals arrived from a location called Hawaiki, bringing 'war, quarrelling and strife' with them. They eventually overwhelmed and annihilated the earlier people, driving surviving remnants into the forested seclusion of inhospitable high country. This mass genocide or the early civilisation occurred within a span of only few centuries preceding colonisation of New Zealand by the British.

Figure 17: An artists rendition of what Miringa te Kakara's Crosshouse once looked like. Drawn by W. A. Taylor.
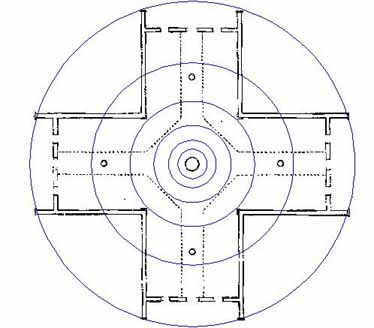
Figure 18: The introduction of the PHI diminishing concentric circles. The outer circle that defines the internal geometry of the Crosshouse has a diameter of 55 feet. This equates to an outer rim circumference of, essentially, 172.8 feet (the diameter of Silbury Hill was 550 feet and intended to code a 1728 feet circumference. The perimeter value of the Great Pyramid was 1728 Royal Cubits of 21 British Standard inches each). Note how the 3rd inward circle brushes the 12" X 12" L shaped corner pieces (ref. "e"), which were custom fitted to allude to this PHI circle, as well as another relationship to do with the intersections of the 8-pointed star. Note also how the 4th inward PHI circle falls onto the edge line of the internal walkway through the building (ref. "f"). PHI relationships also occurred on the large centre post, where its radius, expressed in feet, coded the reciprocal of 1/2 PHI (1.236068045 feet). This means that its circumference was coded to be 93.1975529 inches, which is either 57.6 PHI inches (1.6180339 British Standard inches per PHI inch) or 2.88 Megalithic Yards of 32.360678 inches each. This centre post circumference also coded 115.2 segments in 1/2 PHI inches. (Note: 1152 is a highly significant ancient astronomical number found on most sites). The outer circumference value of the large circle encompassing the entire building was 172.8 feet, which is 5.76 inches per degree of arc or 2.88" for each 1/2 degree. Alternatively, each 2 degrees of arc was 11.52 inches. This means that the outer circumference of the Crosshouse was designed to be 1/756000th of the circumference of the Earth under the ancient, sexagesimal geodetic system. Remember, one side of the Great Pyramid had a length of 756 feet.
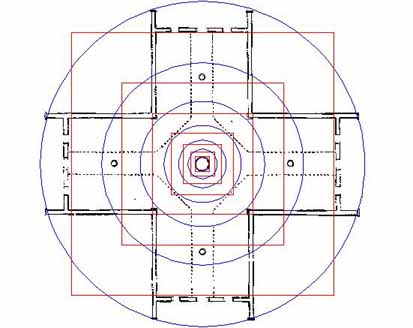
Figure 19: Whenever there are PHI circles they are accompanied by PHI squares and the diameter of the overlaying square will always be 1/2 PHI less than the diameter of the circle. Note how the outer square relates well to the internal lengths of each wing of the Crosshouse. Because the circle diameter is 55 feet (55.0038197097 feet...172.8 ÷ PI), the diameter of the outer square is 44.49902245989 feet (44.5 feet), which is, essentially, 1/4th of the diameter of "Y" Holes at Stonehenge or 1/8th of the PHI coded length of the Menkaure Pyramid (356 feet when read in PHI increments & 357 feet by standard readings). The 3rd inward PHI square (diameter 17 feet) designates the exact positions where the outer walls of the building make their 90-degree turns.
Figure 20: The 8-pointed star introduced to the Crosshouse and sized according to the 55 feet diameter circle (blue) that sweeps past the facia plates at the end of the north and south wings. The builders of the Crosshouse used the facia plates to extract an additional code that interpreted the most extreme sweep of the building (east-west) as 56 feet diameter (outer rim red circle). This was to code 56, in the same way as the 56 post positions of Stonehenge, used for lunar calculations, as well as the Sabbatical calendar count. This clever use of two similarly sized circles also identifies two of the geodetic, Earth navigational systems in common usage. The 55 feet diameter circle (11 series) produces a 172.8 circumference, which was sexagesimal (6 series) and able to be easily calibrated to degrees, minutes and seconds of arc. The 56 feet diameter circle (7 or 8 series) produces a 176.0 circumference, which is an 11 series calibration used in the league, mile and furlong geodetic system. It will be recalled that the British Standard mile was 1760 yards of 3 feet each. The Crosshouse, therefore, under this 176 feet circumference code, would be 1/30th of a mile in perimeter value. With the 8-pointed star in place, these two outer circumferences hold codes according to 1/8th part of the overall circumference. In the guise of 172.8 feet a 1/8th segment is 21.6 feet. This is in recognition of 2160 miles (the diameter of the moon) or 2160 years (the time it takes the Sun to move through one of the 12 houses of the zodiac in the Precession of the Equinoxes (25920 years ÷ 12= 2160. The 2nd calibration (176 feet) designates that there are 22 feet between ray points of the 8-pointed star. This is 4 fathoms (original fathoms were 5.5 feet) or 1/3rd of a chain.
Note how the 8-pointed star fits within the building. Its diagonals intersect with the edges of the "L shaped" corner mouldings and it becomes obvious why they were fitted. The external corners of the four "L shaped" mouldings appear to have been made to relate to the 3rd inward PHI circle and this would account for the thickness of the mouldings. Note how the diagonals forming the north, south, east & west rays of the 8-pointed star converge onto and intersect with the central walkway adjacent to the 4 entryways. With the establishment of this star pattern the layering of the other star and cross patterns can begin.
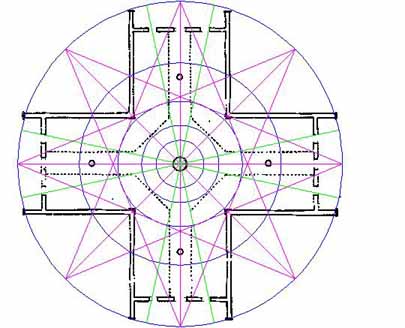
Figure 21: The diagonal lines that make up 1/2 the Grand Cross pattern are introduced and they sit 12 degrees each side of the primary points of the compass. Note how they brush the sides of the window openings as they exit from the building. Note also the points on the internal walkway edges where the Grand Cross vectors traverse, indicating where the walkway reverts from 45 degrees to align with the primary points of the compass.
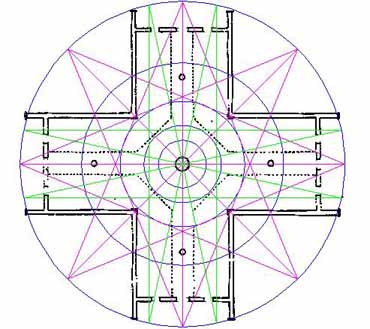
Figure 22: The Grand Cross fully in place and providing intersections for the next star pattern.
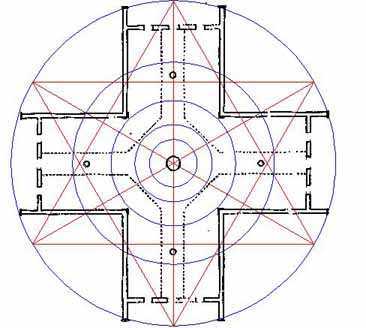
Figure 23: The 6-pointed star, which was used in the North Island of New Zealand for marking the rise & set solstice positions. Note how intersections on the star mark the internal limits of the building within the north and south wings. The external limits of the building, east and west are marked by a conjunction of the star's ray point vectors with the 2nd inward PHI circle. The star will now be doubled to form a 12-pointed star.
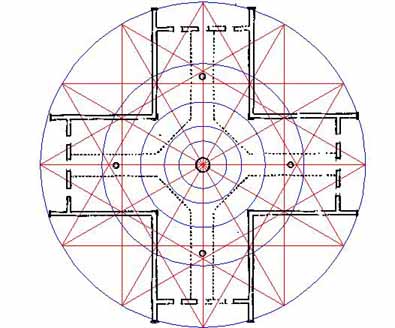
Figure 24: The 12-pointed star, used throughout the world to designate the 12 positions of the zodiac constellations around the ecliptic. Note how the 4 secondary posts are "boxed in" by vectors of this star and how star intersections relate to the positions of the Crosshouse walls.
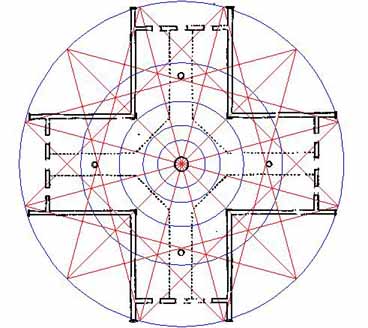
Figure 25: The same 12-pointed star pattern swung 15 degrees of north, south, east and west. Note how the ray point vectors interrelate with the walkway of the Crosshouse and traverse where the walkway turns 45 degrees toward the primary points of the compass. Note also how lines brushing the 4 secondary posts carry on to dissect the internal corners of the porches, on the outside of the building. Return lines run through the corners of the windows.
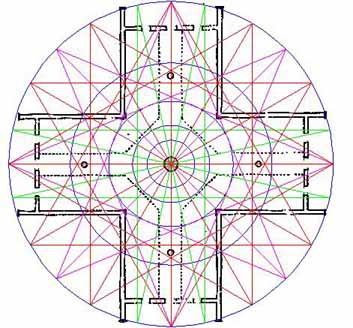
Figure 26: The "all in" geometry so far. Take very careful note of the way that intersections within the star & cross patterns provide for the next ensuing layer. There is no human manipulation of these patterns to force a "fit" as the geometry is self-generating and placed solely in accordance with existing intersections.
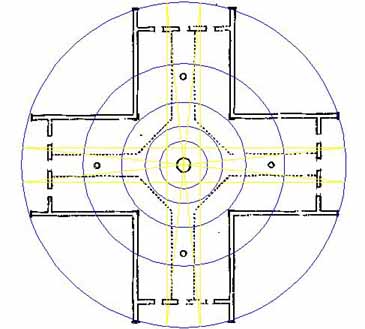
Figure 27: The thin cross with the cross points residing 6 degrees each side of north, south, east & west. Note how the central square of the cross is perfectly framed by the 5th inward PHI circle. Note also the position where the diagonal vectors conjunct with the 2nd inward PHI circle and the edges of the walkway, simultaneously.
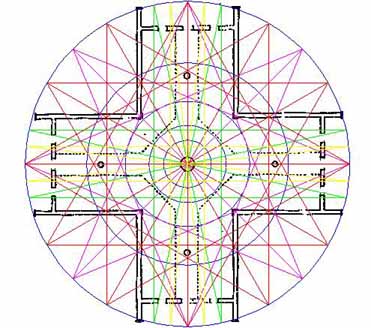
Figure 28: With the thin cross in position many more relationships and intersections between it and the other layered, star & cross pattern geometry can be seen.
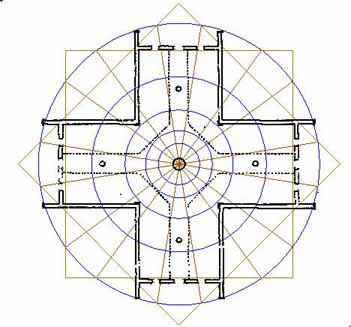
Figure 29: The cobweb of star & cross patterns is momentarily set aside to introduce, with visual clarity, the Holy rectangles vectors. A double set are here shown, but generally, there would only be 8 such vectors running to 36, 54, 126, 144, 216, 234, 306 & 324- degrees respectively. The 2nd set shown run to 9 degrees each side of the primary points of the compass. Note how they relate to the sides of the window openings and when framed within squares, run back through the internal corners of the porches on the outside of the building.
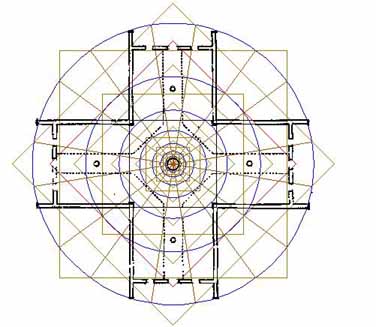
Figure 30: A more complete display of how concentric reductions of circles and squares diminish inward to the centre post. The 2nd inward PHI circle has been framed within a square of the same diameter (red). Note how the square relates to the walkway width at each doorway of the building, as well as to the corners of the doorway itself. The PHI reducing circles and squares finally converge onto the carefully fashioned and sized centre post, which appears to have coded the reciprocal of 1/2 PHI in its radius measurement.