SETTING UP A GROUND-MARKED TEMPLATE FOR ANGLE COMPUTATIONS AND TRIGONOMETRIC CALCULATIONS ONTO DISTANT TARGETS.

Before the sprawling, standing stone array could be set up with the obelisks in their purpose-placed, precise positions it was needful to create a ground template from which accurate degree angles could be computed. That template was based upon the geometry of the Great Pyramid, which opened up the following, accurate surveying possibilities:

Method 1.

By conventional trigonometry, based upon half the Great Pyramid’s length (378-feet) and a face (hypotenuse) slope angle 51.84-degrees, the calculation formula is: 378 ÷ 51.84 cos = 611.789461540 for the length of a diagonal face.

This is then multiplied by PI @ 22/7 = 1922.7668791268550-feet for the circle circumference. When this value is divided by 360-degrees the length of 64-inches is 1-degree of arc to a tolerance of 1/11th of an inch. This would be an easy-to-read and calculate number to work with when calibrating a 360-degree compass circle, where every 5 & 1/3rd feet (64-inches) represented 1-degree.

Method 2, where modern approaches to calculating in Sine, Cosine & Tangent trigonometry is not necessary.

Virtually the exact same result can be achieved by using the PHI ratio of 1: 1.6180339. Therefore 378-feet X 1.6180339 = 611.6168142 (a mere 2-inches shorter than by the first method). When this diagonal length value, used as a radius value, is multiplied by PI @ 22/7 the circumference generated is 1922,2242732-feet or essentially the same 64-inches per degree of arc, but this time to a tolerance of 1/14th of an inch. This also equates to 3.3 PHI feet (1-foot X 1.6180339) for each arc shift of 1-degree.

Of course, the option was also available to create circles with a radius of 756-feet that centred on either the hubstone or its counterpart, situated 756-feet away at the opposite end of the baseline to the NNE. Such a radius would create a circle with a circumference of 2376-feet (using PI @ 22/7th). On this circle, every 6.6-feet (79.2-inches*) would represent 1-degree of arc shift).

*Note: The increment of 7.92-inches was known as the “link” and was widely used in surveying into modern times before the unfortunate introduction of metrification. The link was 66/100th of the surveying increment called the “chain” and there were 80 chains to the mile (5280-feet) or 8-furlongs/furrowlongs (660-feet).

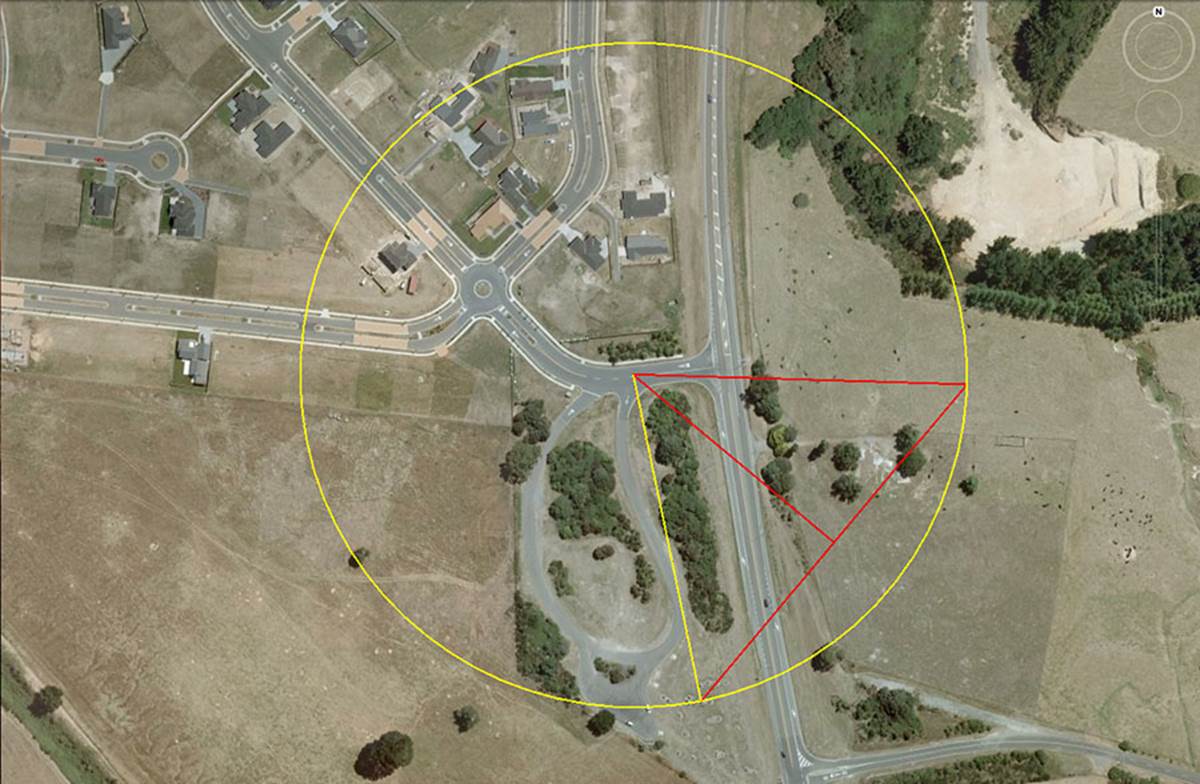
Within the ancient, ground marked 2D pyramid geometry, all 3 corner points could be used to determine accurate angles to targets through 120-degree sweeps of the horizon, respectively, using the straight line vector of a pyramid side or base opposite, housed within a circle.

Method 3, the apex circle.

In the above picture a PHI based circle emanates out from the apex to touch the corners of the ground marked pyramid geometry.

Because the diagonal side (face) length is the product of 378-feet X 1.6180339 = 611.6168142-feet (to all intents and purposes the same length as generated by a 51.84-degree slope angle) the PHI ratio of 1: 1.6180339 comes into play. Therefore, if the face line from the apex to the base is drawn inwards 1-foot along the baseline, the length of the sloping face (hypotenuse) decreases in length accordingly, whereas the base length decreases from 378-feet to 377-feet, and so forth.

This condition continues for 378 feet until the vertical centre line from the base to the apex is reached, at which point the hypotenuse line begins to increase again marginally with each additional sideways vector shift of 1-foot along the 756-feet baseline. This subtle shortening or lengthening of increments along the baseline would be recorded and become the basis for log numbers in angle computations.

At the same time the original length of the face (hypotenuse) of 611.6168142-feet continues to act as the radius of the circle produced from it. In this circle, each 10.66666-feet* (128-inches) of shift = 1-degree of arc to a tolerance of 1/81st of a foot or 1/7th of an inch.

*Note: 611.6168142-feet would be equivalent to 226.8 Megalithic Yards, if Scottish engineer, Professor Alexander Thom’s, estimate for a Megalithic Yard was off by a mere 1/300th of an inch (visually undetectable). He found a recurring measurement on Megalithic sites that he averaged to 89.2 centimetres and this would equate to 32.6378-inches. However, ancient civilisations were using PHI-inches (1-inch X 1.6180339) or PHI feet in their calculations, as well as copious use of the PHI reciprocal in the form of 10-inches ÷ 1.6180339 = 6.18034-inches*. 

Professor Alexander Thom’s Megalithic yard was assuredly based upon 20-inches X 1.6180339 = 32.360678-inches.

*Note: The PHI reciprocal formula was essential to “squaring the circle” when producing capacity tubs for selling quantities of grain or dry-goods in ancient marketplaces.

For example, the ancient English bushel was intended to be 2160 cubic inches.  The old English Winchester standard described a bushel tub as: "any round measure with a plain and even bottom, being 18.5 inches wide throughout and 8 inches deep". This was a slightly “drifted” capacity by the time the standard was written, but was obviously, originally based upon 3 X 6.18034-inches or 18.54102-inches.

Therefore: Using PI X the radius squared, the result is: 6.18034-inches X 3 = 18.54102 inches ÷ 2 = 9.27051-inches (squared) = 85.94235566 X PI = 270-square inches X 8-inch high sides above the round base = 2160 cubic inches.

All ancient measures of the cousin civilisations had to contain codes in their capacity values. In this case it was 1/12th of the 25920-year duration of the Precession of the Equinoxes, where the sun spends 2160-years in each House of the Zodiac. Coincidentally or not, the diameter of the moon is 2160-miles.

*Note: The ancient French Pied du Roi was 1.0666666-feet or 12.8-inches.

Method 4, the truncated pyramid circle.

Similarly, throughout all recorded history the Great Pyramid was a truncated pyramid with a flat floor, 44-feet square, situated at a vertical height of 453.6-feet. This height complies with 280 rounded PHI feet of 1.62-feet each (19.44-inches) or could be read as 280 X 1.6180339-feet to a tolerance of about 1-inch. With the base length of the Great Pyramid (756-feet) being 9072-inches, the half value is 4536-inches (378-feet).

There was, therefore, yet another option available to the ancient savants-surveyors of Wharewaka, Taupo to create a circle at 90-degrees to the centre baseline that ran towards the apex of the pyramid geometry, representative of where the flat altar floor sat atop the Great Pyramid. Therefore, a circle based upon a radius of 453.6-feet X PI @ 22/7th would generate a circumference of 1425.6-feet. This would mean that each 3.96-feet (47.52-inches) would represent 1-degree of arc shift around the circle.

Of course, 3960 is half of 7920 (the diameter of the Earth in miles of 5280-feet each). Also, the sum of 47.52-inches is simply 6 “links” of 7.92-inches, used in traditional British surveying practice since time immemorial.

Method 5, the full height pyramid circle.

And again, the savant-surveyors had the option to run yet another circle from the apex obelisk to the centre baseline position situated 378-feet @ 90-degrees from either the hubstone or the pyramidal obelisk opposite at the other end of the baseline. Trigonometry dictates that the vertical height of the Great Pyramid, complete with its capstone, would have achieved 481 & 1/11th feet to a very close tolerance.

Using this value, the circle generated by this radius, again using PI @ 22/7th, would be 1512-feet in circumference. Of course, this circumference is 2 X 756-feet (the length of the Great Pyramid at its base and 1/8th of 1-minute of equatorial arc for the world). In this circle each 4.2-feet (50.4-inches) would equate to 1-degree of arc shift.

These comparisons or ratios between the shortening of the hypotenuse, concurrent with the shortening of the baseline in a triangle, became the basis for creating logarithmic charts for trigonometric calculations. Using all 3 sides of the 2D Great pyramid, orientating out in 3 directions and covering 120-degrees of horizon each, allowed the ancient people to do accurate distance and angle calculations to determine just how far away horizon targets were.

Beyond setting up this very accurate and versatile template the ancient surveyors of New Zealand would have used long knotted ropes* to set out their geometric patterns or the compass circles derived from the geometry. In ancient Egypt such surveyors were called “rope stretchers” or “harpedonaptai”.

*Note: In ancient New Zealand complex numbers were recorded by specially tied knots on strings. These devices were called “kupu” or aho ponapona or aho tiponapona (also tau ponapona) meaning “many knotted cord”. In the oral traditions of the Maori wharewaananga (school of ancient lore) these were also known as the “string knot language”. The same devices were used in South America for recording complex numbers and, in Peru as elsewhere, were called “khipu or quippu” … phonetically the same as “kupu”.

The kupu devices used by the ancient New Zealanders were sufficient to record the many refined logarithm numbers used for accurate surveying and angle calculations.

The half scale, two dimensional, Great Pyramid geometry at Stonehenge.

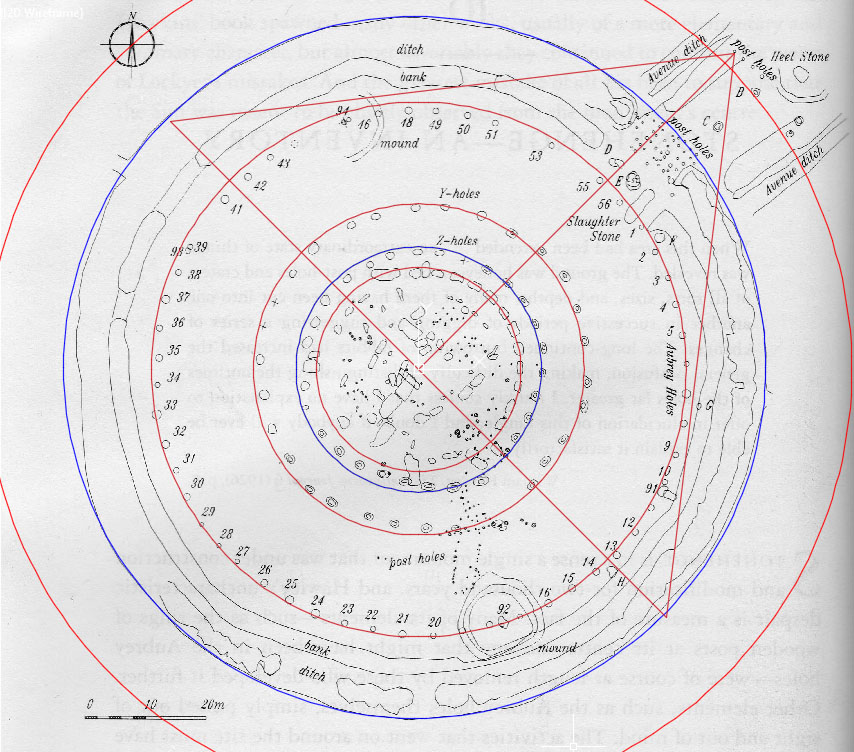
It seems apparent that Stonehenge was originally laid out using a half-scale, Great Pyramid template. The above picture is in perfect scale.

As with many other megalithic sites, some circles within Stonehenge are slightly elliptical. However, a 378-feet diameter circle (blue) encases the Stonehenge site virtually perfectly from outer-ditch-edge to outer-ditch-edge across the entire site, excluding only the more extended Avenue and Heel Stone.

A stone marker designated as “H” in the above scaled plan delineates how a pyramid base line goes from 135-degrees to 315-degrees from the edge of the outer ditch, across the embankment, through the site’s epicentre, across the opposite embankment to finally resolve at the outer ditch edge 378-feet distant (half the length of the Great Pyramid).

At the same time, a line commences centrally at 90-degrees opposed to the pyramid baseline and runs for 240.5-feet @ 45-degrees to resolve against a post on the Avenue. En-route it dissects a Sarsen obelisk, as well as post positions on the Z-Holes Circle, Y-Holes Circle, brushes a post on the Aubrey Circle, runs between stones D & E, dissects a post row and resolves upon an end post near the Heel Stone.

On the southwestern side the pyramid hypotenuse line brushes past recumbent marker stones, now tumbled off the top of the embankment to lie slightly off-line, brushes the Aubrey Circle, brushes stone "C" to then resolve on the end post.

The evidence suggests that this pyramid geometry at Stonehenge was set up to be swivelled in order to place the apex of the pyramid template onto each of the 4 posts at the apex (a 5-degree spread). All of these determinations would have been accomplished by “rope stretchers” or “harpedonaptai”.

With regards to ancient surveyors deliberately making ancient circles elliptical, Professor Alexander Thom stated:

'builders occasionally distorted circular monuments, to make the relationship perfect and that this is at the root of the custom of creating oval rings' (see: Stonehenge, Neolithic Man and the Cosmos, by John North, pg. 302).

The Sarsen Circle at Stonehenge was slightly elliptical in order to carry 90-degrees opposed diameter codes. The diameters of the Sarsen Circle inner ellipse are 100-feet, and then, 90-degrees opposed, 100.8-feet respectively, Whereas the 100-feet diameter rendered a circumference of 314.16 (coding PI X 100), the 100.8-feet diameter was 1-second of equatorial arc for the world’s circumference.

Further to that, the Great Pyramid is erroneously purported to have been built about 400-years after Stonehenge, when in fact all the evidence proves it’s as much as 10,000-years older (or more).

The PHI ratio at Stonehenge.

Unsurprisingly, the PHI ratio is well-represented at Stonehenge in the concentric circles of the site. This preoccupation of using the PHI ratio thus duplicates methodologies of the ancient surveyors at Taupo, New Zealand.

The Aubrey Circle (red) at Stonehenge has a coded diameter of 288-feet, converting to a circumference of 907.2-feet using PI @ 3.15.  Of course, 9072-feet would equate to 1 & ½ minutes of equatorial arc for the Earth. Likewise a mathematical progression, based upon 288, generates a string of highly important numbers used in ancient navigation, etc., and the Egyptian Pyramid Acre was 28800 square feet.

The 288-feet Aubrey circle ÷ by PHI @ 1.6180339 produces the next inwards concentric circle called “Y”-Holes (red) @ a coded diameter of 178.2-feet (to a tolerance of 2.4-inches).  This diameter value sets up a mathematical progression that generates a raft of numbers related to navigation, precession, etc.

The Y-Holes Circle is reduced by PHI to generate the concentric ring that encircles the outer rim of the Sarsen Circle (red), with a diameter of 110-feet. This is an “11” family value that relates to navigation by the mile of 5280-feet. This family of numbers used PI @ 1728/550th to generate whole number circumference readings, thus it converts to 345.6-feet for the outer rim of the Sarsen Circle. The sum of 345.6-miles would be 1/72nd of the 24883.2-mile equatorial circumference or 5-degrees of arc.

The Z-Holes Circle (blue) in the above scaled picture that stands outwards from the Sarsen Circle is 132-feet in diameter. It is not a PHI reduced or generated circle, but is based upon the “11” family of numbers (12 X 11). Again it relates to navigation by the mile of 5280-feet and 132-feet = 1/40th of a mile. This diameter converts to 414.72-feet using PI @ 1728/550th and 414.72-miles would be 1/60th of the 24883.2-mile equatorial circumference.

Added to the above, there was yet another PHI circle (red) outwards from the Aubrey Circle, the limits of which were marked by stone “B” on the Avenue. This position generated a circle diameter of 466-feet using pure PHI @ 1.6180339 or 466.56-feet using “rounded” PHI @ 1.62. The intention was to capture the number 466.56-feet. Under the 130636800-feet assignment for the equatorial circumference of the Earth (12 X 12 X 12 X 12 X 1.2 miles of 5250-feet each) the sum of 46656-feet would be 1/2800th part.*

*Note: The sum of 933120-grains (466560 X 2) was the ancient Sumerian-Babylonian Talent weight.

Much more could be said about the mathematical relationships, numbers used and self-same measurement or angle standards shared between these, half-a-world removed sites, but Stonehenge is not the focus of this article.

MOUNT TAUHARA AND THE WINTER SOLSTICE ANGLE

From the hubstone, at the time of the winter solstice, the “first glint” of the sun can be seen to the right hand base of Tauhara’s centre cone hump. The sun climbs the hump edge to finally bath and obscure the whole crater in a blaze of light.

About 612-feet away from the hubstone at the apex of the pyramid geometry was the giant obelisk with its seat facing Mount Tauhara. It seems obligatory that observations were being made onto the winter solstice “first glint” position from that end of the hypotenuse line (a surveyor’s baseline of precise known length). For calculating overland distances by trigonometry, one needs a surveyor’s baseline from which degree angle readings to the target are made from each end of the line.

Other advantages of using a 2D Great Pyramid template for standardised trigonometric calculations.

The length of the Great Pyramid @ 756-feet of 12 (so-called) English inches converts to increments used or shared by the ancient cousin nations:

Therefore, 756-feet is also, 720 Greek feet of 12.6-inches; 360 Assyrian cubits of 25.2-inches; 432 Hebrew/ Celtic royal cubits of 21-inches, 504 Hebrew/Celtic common cubits of 18-inches; 540 Hebrew “cubits of a man” of 16.8-inches; 72 Hebrew/Greek reeds of 10.5-feet; 1.44 Greek short stadia of 525-feet; 1.2 Greek long stadia of 630-feet;  777 & 7/8ths Roman feet of 11.664-inches, 155 & 5/9ths Roman Paces of 58.32-inches, etc.

There was obviously a Roman overland foot of 11.666666-inches (11 & 2/3rds) and Pace of 58.33333-inches. There would be 777.6 Roman overland feet in 756-feet or 155.52 Paces. Note: the sum of 1555.2-miles equates to 1/16th of the 24883.2-mile equatorial circumference. The half value of 1555.2 is 777.6.

Then again, 3 variations of the Egyptian Royal cubits fit the code-bearing dimensions of the Great Pyramid under its 756-feet or 756.25-feet assignments.  There was also a symbolic PHI length (560.6 X 1.6180339) or a literal rounded PHI length (560 X 1.62 –feet).

Beyond that one needs only to look at the most ancient European measurements, ranging from the British Isles, Atlantic seaboard countries and ranging across into Eastern Europe to see they were/are in direct ratio to the Great Pyramid’s dimensions. Here’s a link to ancient Swedish standards: http://www.celticnz.co.nz/VikingNavigation.htm

IN SUMMARY.

Up until recent years there was an expansive, fully-fledged, mostly surviving standing stone array at Taupo, which had been built by the ancient inhabitants, undoubtedly, a century or two after the 186 AD volcanic explosion that devastated the area. Huge effort went into moving massive obelisks to precisely pre-determined positions and erecting them to stand unnaturally upright.

Each outer-marker obelisk contained at least two codes of position around from due north, one of distance and one of angle. Both the measured distance out from the hubstone and the angle number generated within a 360-degree system, produced encoded scientific numbers that were needful for the establishment and maintenance of civilisation and abundant society. The cyclic-astronomical, navigational and lunisolar calendar sciences were encoded by a parcel of highly specialised numbers in strings or progressions.

Unfortunately, our archaeologists and other disciplines of experts were not sufficiently trained or interested to see, what was so glaringly, in-plain-sight before their eyes at Taupo, so let a world-class, archaeological site, almost on a par with Avebury Henge in Southern England, be destroyed. Small sections yet remain to demonstrate what was there in much greater profusion, but the once expansive site now reduced to a mere shadow of its former glory.

This is a sad loss for New Zealand and the worldwide research community.

Martin Doutré, 30/9/18.©

With special thanks to Graham Parminter, who remained eternally vigilant in trying to alert others about the obvious archaeological and historical importance of this site.

To be continued.