WHY DID EUROPEAN NATIONS, FROM REMOTEST ANTIQUITY, SET UP STANDING STONE CIRCLES OR CODE BEARING STRUCTURES AND ALIGNMENT MARKERS EVERYWHERE THEY WENT?
Complexes of standing stones, such as the great lines of obelisks at Carnac in Brittany, France, or at Avebury Henge in Southern England, etc., were great libraries of very important coded mathematical information. There was never anything mysterious or magical about this and the information could be extracted at any time by anyone who was reasonably adept at using a standard measurement rule or who could determine a precise degree angle off north. The observer stood at the central hubstone of the site and determined the distance and angle to outermarker stones. The sought after scientific information was contained within the separate values of distance and angle to the outer target position, This dynamic ancient information still reposes in those stone positions and can never be erased until the stones are moved or eradicated. Thankfully, at Avebury Henge in Southern England, although many stones were destroyed by over-zealous Christians, the depressions where the stones once stood remain, so the original codes are still delicately and tenuously intact for the moment.
The best repository of this standard coded information, so-far encountered by this researcher anywhere in the world, is within the lengths and angles at Nazca Peru. There are, literally, many hundreds of lines, some of considerable length and the longer the line the more refined a degree angle code becomes. Even a minuscule .1 of a degree of adjustment to an angle over a long length can throw a test line off its established target by a wide margin. At Nazca, the sheer length of many geometric drawings leaves little opportunity for fudging the results and making them comply to a preconceived notion. If any lines sit at arbitrary and meaningless angles, then that would be immediately apparent. As it turns out, the values generated are wonderful, factorable numbers of great significance, which work well in mathematical progressions.
The mathematical information encoded into European sites was essential and central to their concept of "civilisation" and ordered, abundant society. Without these hard-won scientific values, civilisation could rapidly decline to the worst case scenario of total anarchy, survival of the fittest and even to the lowest of vile human conditions... rampant cannibalism.
There was a revered and sustained mathematical parcel, handed down religiously from forebears, that the carriers and trustees of "European-type" civilisation needed to know and keep at the forefront of memory, generation upon generation. The information included:
In each generation, teachers were rigorously trained in all of the scientific arts to be handed on to the ensuing generation. Huge open air universities, like that of Nazca or Avebury Henge, were built and then enlarged upon as the generations passed. It's quite obvious that, at Nazca, more and more tutorials were added over the years and that anyone issuing forth from the great sprawling school graduated, potentially, as a highly trained individual who had thoroughly learnt the navigational and cyclic numbers by rote, constant hands-on practice and grueling repetition. To read Julius Caesar's descriptions of advanced shipwright skills in his day and the great Druidic schools of Britain where navigational mathematics, astronomy or "the size of the Earth and its divisions" etc., were being taught, CLICK HERE

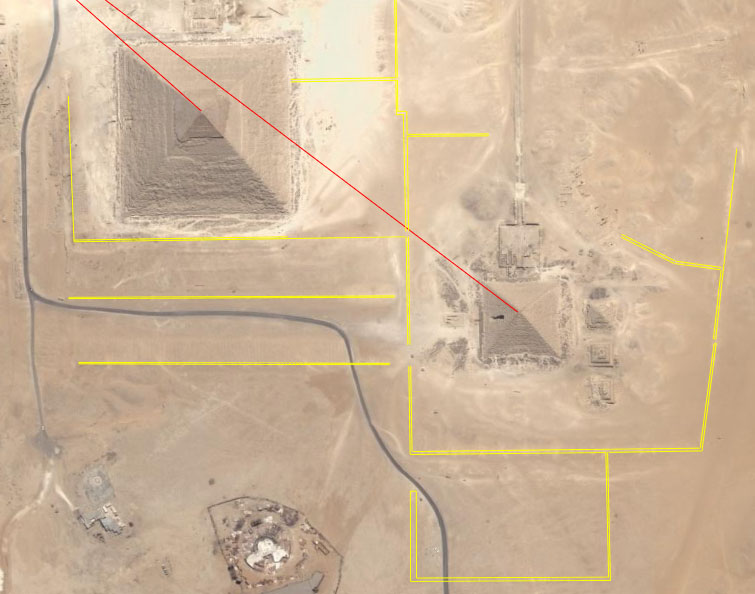
Long before the Nazca desert was etched with code bearing geometric designs, the desert terrain around the Pyramids of the Gizeh Plateau of Egypt was similarly set out in semi-abstract looking, code-bearing patterns. Each set of meandering lines seen here in the vicinity of the Khafre and Menkaure Pyramids carries profound scientific information by way of length and angle and is ideally suited for teaching initiates the astronomical and navigational arts. Along with this ground geometry were the pyramids themselves, as well as the many temple edifices or causeways, where every length, height, width, angle, size of a window or door, pillar count, etc., contained a tutorial. This exact, self-same information, encoded using the same measurement standard and Sumerian-Babylonian 360-degree system, is found at Nazca, Peru. Meandering, code-bearing walls like this are found at Cahuachi pyramid complex, situated only a few miles SSE of the Nazca desert geometry
So, let's now begin the huge task of deciphering the codes built into the desert at Nazca, Peru, which were placed there to teach ancient students principles of navigation and positional plotting at sea, the lunisolar calendar system or cyclic astronomical arts of solar, lunar, planetary and stellar rises and sets.
A STARTING POINT
Within the huge complex of Nazca patterns we need a starting point for indepth analysis, which will be founded on milleniums-old standard surveying methodologies and practices, so here's one:

Here's an interesting looking candidate for in-depth analysis... a rectangle with a couple of trapezoids running through it and secondary lines running off or through the more distinguishable clumps of geometry. Then there's the long diagonal line running towards another major geometric configuration almost a mile away to the southwest. The main rectangle has clearly seen cairn surveying markers at each end, so they'll be the benchmark stations that the ancient surveyors worked from when setting out the "distance and angle" design for this particular site. Let's go closer in and make a start.

Red arrows point to the two surveying "benchmark" cairns of the giant rectangle from which the secondary positions of "backsights" are determined. A series of yellow arrows point to a few of the many marked interim stations or to the corner positions where the secondary geometry begins. The reason that the huge geometric patterns at Nazca are so abstract is that every line and every angle incorporated into the designs had to carry codes for teaching initiates important scientific principles. The teaching methods found in this first huge geometric configuration, apply equally to all of the other patterns, spread out for miles over the surrounding landscape and once the basic method is learnt, then "cracking" Nazca is quite easy. Let's now use the centre of the eastern marker cairn to see if there's any recognisable value in the choice of distance and angle to a randomly chosen corner position.
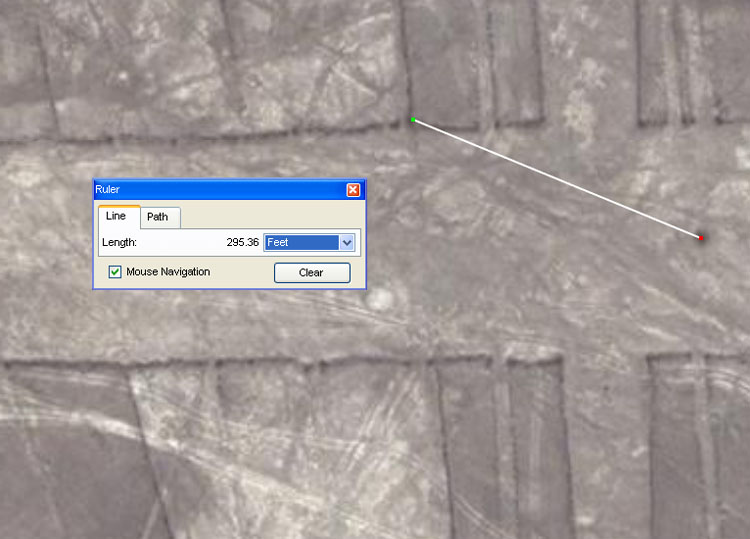
The ruler tool in Google Earth appears to provide excellent relative accuracy at the Nazca site. The algorithm that its designers have incorporated would need to be very precise or the known latitude and longitude coordinates of towns and geodesic trig stations in the region would very quickly distort. Google Earth satellite imagery and accuracy is sufficient to complete this analysis very adequately. In the above picture a sample line is shot from the cairn centre to an indented mark in the corner, where there is a conjunction between the main rectangle and trapezoid. The distance is fairly represented as 295.3 feet. Once this line's angle is tested within the exacting confines of AutoCAD it proves to be 291.6-degrees. So, with these initial distance and angle values in hand we can ask, 'what were the ancient Nazca astronomer-navigator-mathematicians trying to code there in the corner'? The detailed answer that follows will be a sample precursor to every other design feature of this entire, vast complex of geometric designs and the thousands of coded stations spread out over hundreds of square miles.
The distance was meant to represent 295.3125-feet (295 & 5/16ths) and this is a very important lunar value much used in the ancient Mediterranean and Europe. Consider the following:
Although severe critics would argue that accuracies down to 5/16ths of a foot are unachievable in this exercise of measuring a length from satellite imagery at Nazca, the same argument cannot be applied to degree angles, especially on very long lines. The fact is that very recognisable degree angle numbers, from the standard parcel of codes found on British and Mediterranean sites, occur repeatedly in each and every azimuth of Nazca and this lends credence to the use of these values in linear measurements as well. After the length and angle values of a few thousand of these lines are positively identified and recorded, then that sheer accumulation and repetitious use of specific values like the above will show, beyond dispute, precisely what was encoded into the Nazca landscape.
The angle of this sample line is, as stated, 291.6-degrees or 291.6666666. Consider the following:

Here's the site we'll be working over, shown in an oblique, diagonal view from an overflying aircraft or from the cliffs above the site. Note the two surveying cairns (black dots) situated at each end of the rectangle. The distance and angle between the cairns contain dynamic numerical codes, much used by the European cousin nations since remote antiquity. The values encoded are found, repeatedly, on edifices or sites from the Eastern Mediterranean countries to Continental Europe and Britain. The early, predynastic mummies of Egypt, like the Nazca mummies, were Caucasoid-European ethnicity in their physical anthropology. Hence, the values found at Nazca parallel those of the highly mobilised and voyaging ancient European cousin nations, who scattered abroad from their Mediterranean-European homelands and set up ancient civilisations on many continents. Photo from The Mystery of the Nasca Lines, by Tony Morrison, 1987. For further insights into the ethnicity of the pre-dynastic and early dynastic Egyptians, CLICK HERE
POINT 1:
Before we proceed further it's very important to establish a point with tremendous clarity: The Great Pyramid & Khafre Pyramid of the Gizeh Plateau of Egypt, along with other structures and features on that huge site, once represented the CENTRAL BUREAU OF STANDARDS FOR THE COUSIN MEDITERANNEAN-EUROPEAN BASED NATIONS. Specially chosen emissaries or representatives of the scattered cousin nations could return to Egypt's Gizeh Plateau, periodically, to check the integrity of their Weights, Measures and Volumes standards or have new sets of rules, volume tubs and vessels or weights issued to take back to their nations. The fact that the standard mathematics of Egypt are centrally important to Nazca in Peru, as well as to the worldwide distribution of sites where the cousin nations settled in remote antiquity, will become more and more apparent as we proceed. For an article showing, irrefutably, that there was ancient, ongoing contact and trade between Egypt and the Peru-Bolivia region of South America, CLICK HERE
POINT 2:
The "INCH" that
has come to be known as the British standard inch is millenniums
older than the British people and is the same inch from which all of the CUBITS
or FEET of the ancient cousin
nations were derived. All are expressions of the selfsame INCH
and all of the cubits or other measurements used by the scattered cousin European
nations were in direct, calculable ratio to each other. This point will be demonstrated
exhaustively as we proceed.
Patricia Mason, a leading authority on the geometric earthmound
complexes and burial mounds of Ohio and Pennsylvania, etc., USA, recently made
this researcher aware of the 19th century work of J. Ralston Skinner,
who undertook precise surveys of Ohio's geometric earthmounds. Skinner's conclusion
was that the mound builders of the Ohio Valley had positively used the increment
known as the British standard inch in the design and construction
of the ancient geometric complexes he surveyed. See: Skinner, J. Ralston.
"Identification of the British Inch as the Unit of Measure of the Mound
Builders of the Ohio Valley." Journal of the Cincinnati Society of
Natural History Vol. 9 (July 1886), pp. 51-63.
This journal can be accessed online by going to: Cincinnati
Historical Society Digital Journals
For a mathematical assessment of the Octagon of Newark,
Ohio, See: http://www.celticnz.co.nz/octaone.html
POINT 3:
Perhaps it should be obligatory for archaeologists to spend a few years in the trades, working with measurements, before they subject the rest of us to utterly banal theories about ancient measurement methodologies. In all eras an adept tradesperson will always have a measurement system based upon very factorable numbers. Once a standard length is decided upon, it is then halved, quartered or further subdivided into eights, sixteenths, thirty seconds, sixty fourths, etc. The same standard length, in other related functions, can be subdivided into either twelfths, elevenths, tenths, ninths, sevenths or such things as "rounded" PHI (1.62") or "rounded" PI (3.15") increments, etc.. There was a wide selection of ancient, specialised rules. Some were dedicated solely to lunar calculations, while others were dedicated to navigational functions. Some were solely mnemonic devices. Others were primarily for interpreting circumferences created by a standard diameter from a particular number family. The Greek "Pygon", used in navigation, seems to have been a measurement that fell into this specialised category.
As mentioned, the only measurements that ancient Europeans used in their "civilisations" were based upon very factorable numbers. These are also called "harmonic" numbers and can be a huge number describing the equatorial circumference of the Earth, which is reducible down to an "inch" and then fractions thereof. A tradesperson will never use a "stand-alone", arbitrary or abstract number, which is not factorable, as the basis of a measurement system. A length will start out as a whole number or a whole number and a simple fraction and there will be no unnecessary complexity. All ancient public buildings or edifices of the European civilisations had inbuilt codes that related to the lunar cycles or the equatorial circumference of the Earth, etc.