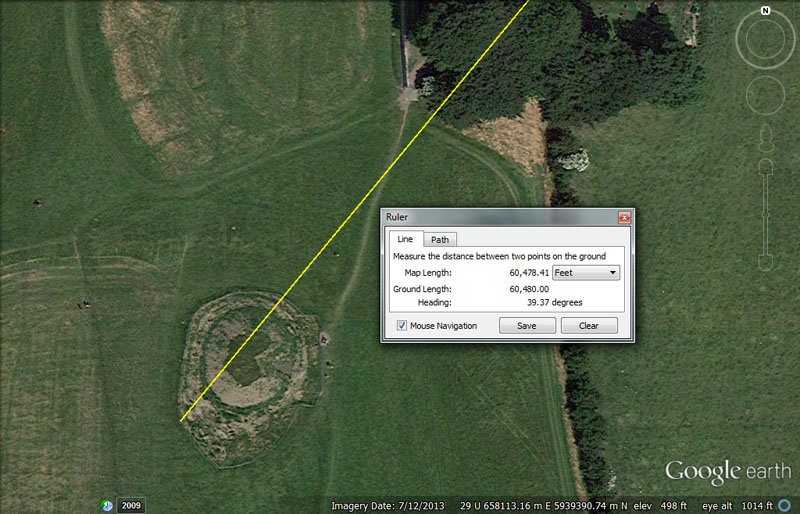
BUT THE MOUND OF THE HOSTAGES WAS ALSO TARA'S TARGET TRIG FROM DOWTH HENGE.

A line extends for 60480' @ a return angle of 39.375-degrees from the epicentre of Dowth Henge to resolve onto the Mound of the Hostages atop the Hill of Tara.
This distance is exactly 10-minutes of Earth equatorial arc or 9 ancient Irish miles of 6720' each. This distance between Dowth Henge and the Mound of the Hostages would be 1/2160th of the equatorial circumference of the Earth (or 60480' X 60 X 6 X 6).
The return angle of 39.375-degrees (39 & 3/8ths) is navigational & lunar coding simultaneously and, in a mathematical progression, generates a range of values much used in ancient calculations.
For example, the lunar year of 354.375-days = 39.375-days (945-hours) X 9 or the increment that later became the Greek stadia (630') is 39.375' X 16, etc.
This giant triangle extends from Dowth Henge to the chambered cairn trig atop Slieve Gullion Mountain to the Mound of the Hostages atop the Hill of Tara and back to Dowth Henge. Each side represents a very accurate surveyor's baseline, configured for readings according to either minutes of arc in the equatorial circumference of the Earth or in ancient Irish miles simultaneously*. From each end of these baselines, yet further triangulations could be made onto targets, sufficient to map the whole country and achieve accurate distance and angle readings to any desired location.
*Note: the ancient value for 1-minute of arc was .9 of an Irish mile.
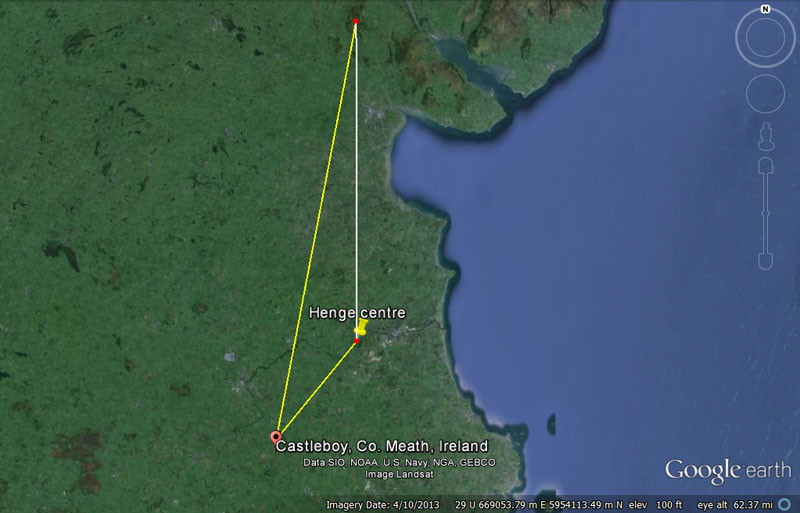
Yet another highly important and accurate, coded triangle existed between Dowth Henge to Knowth chambered mound, triangulating onto An Forradh on the Hill of Tara.
The distance and angle to Dowth Henge from An Forradh's inner sanctum were coded to be 60750' @ 39 & 2/7ths degrees
This distance is, 12.5 so-called Roman miles of 4860'. At the same time it is 10 Roman nautical miles, which was an increment 1.25 larger than 4860'. The nautical mile was, simply, 1-minute of arc (6075') under yet another navigational system that the Romans adopted from earlier civilisations.
Under this alternative method of navigation, 75 Roman miles equalled 1-degree of equatorial circumference arc. Therefore 4860' X 75 = 364500' X 360 = 131220000' or 27000 Roman miles. One arc second under this Roman method was 101.25'
The distance into the inner sanctum of An Forradh could also be read as 60720' (11.5-miles of 5280' or 92 furlongs/furrowlongs of 660' each).
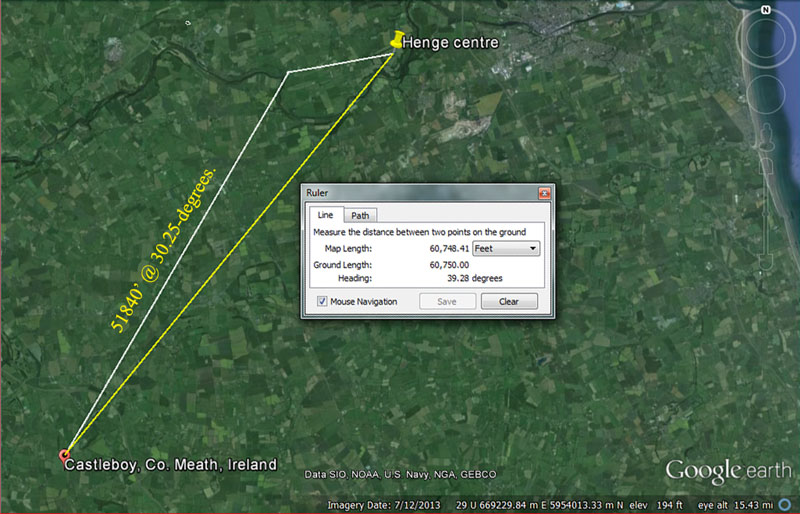
The distance and angle to Dowth Henge from An Forradh's inner sanctum were coded to be 51840' @ 30.25-degrees. The very important attributes of the 5184 value will be explained as we proceed.
SETTING OUT THE SCHOOL OF NAVIGATION.
Now a programme could be commenced to build a huge, sprawling open-air-university, with surveying markers dotting the landscape for miles in every direction. These multi-type markers would fulfil the role of make-believe islands in the sea, which novice students had to find by precise navigation.
Students would be assigned an overland voyage from island-to-island and be told the distance and degree angle to each target from the point-of-departure. The vast majority of readings given for distance and angle to a target would be fully based upon special numbers that HAD TO BE MEMORISED, for within these factorable numbers and their manipulation were the entirety of the sciences related to cyclic-astronomy, the lunisolar calendar, and navigational methods for traversing the featureless oceans of the world.
If one ventured out to sea without this knowledge, they were surely going to die.
After having found the first artificial island objective within the Boyne Valley complex, calculations could be made to mathematically determine where the 2nd objective should sit in the landscape, and so forth. The positions of high trig points or landmarks and the changing angle to them, as the orienteering group moved overland, would act as aids in positional plotting and staying on course.
If the group got lost or confused momentarily, they had means at their disposal to stop, set up a moderately small, lightweight but very transportable device, which later became known as the Celtic Cross, and within 45-minutes or so of sun movement, determine the exact degree angle to any visible target on the horizon.
DOWTH & NEWGRANGE CHAMBERED MOUNDS.
In addition to Dowth Henge and Knowth chambered mound, sitting at each end of the Boyne River Valley, two other giant dormitory complexes were built to accommodate students of navigation and these sat more centrally. The idea was that students could commence their orienteering exercises from at least four scattered locations and, using different distance and angle codes, find the same designated targets and objectives in the outer landscape.
The variety of artificial islands, lying away from these three centralised chambered mounds or Dowth Henge, included simple ring ditch structures to double ring ditches, embanked rings, double embanked rings, round mounds, oval mounds, square-based mounds at offset angles, chambered mounds, cairn heaps, souterrain dwellings, henges, standing stones, standing stone circles, post circles, promontories, etc.
These outlying satellite structures were, themselves, coded by way of diameters and circumferences and very useful tutorials existed within the dimensions of each one, extractable by careful measurements and the use of the PI ratio. A ring ditch, for example, would provide a diameter of, say, 52.5' and this could be likened to a leg of travel at sea of 5250' or, what became, 1-Greek mile. Using PI @ 22/7ths, this (scaled-up) diameter converts to a circumference of 16500' (1-English league or 3.125 or 3 & 1/8th English miles) for which every 45 & 5/6ths feet (550") would represent 1-degree of circumference arc.
It was by this method (legs of travel converted to circumferences divisible by 360-degrees) that positional plotting was done at sea at the completion of each sea leg of travel.
Clues that exist in ancient allegorical-myths suggest that students were divided into groups of about six and then handed their navigational assignment to go, as a group, from here-to-here-to-here and back to base. A circuit could involve finding, measuring and describing a series of sites, either near-in or far-out, depending upon training and ability. It's easy to see that more seasoned and adept students ranged out in ever widening circuits to sites 20-30 miles distant or more.
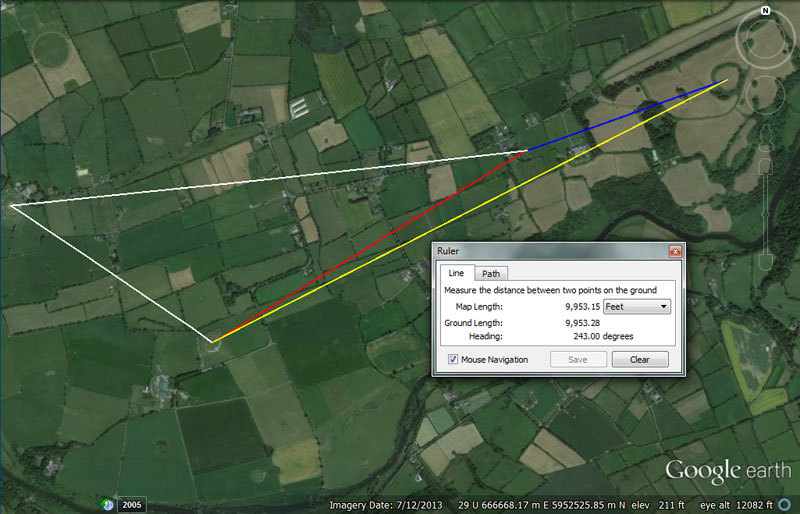
Each end of each line shown resolves onto one of the four primary benchmark positions from which students of navigation ventured out to complete their orienteering exercises. Here's a preliminary glimpse of what the distances and angles between the 4-main structures mean:
(1). From Knowth chambered mound to Dowth chambered mound (upper white line) would have carried the codes of 8910' @ 264-degrees.
The 8910' value is navigational, from the "11" family of navigational numbers that used the mile of 5280'. The length of 8910' is 1 & 11/16ths miles. The sum of 24750-miles X 360 = 8910000.
The mathematical evidence from several British sites attests to the fact that there was an increment used of 24.75-inches (2.0625') which was directly related to the "11" number family based Egyptian Royal Cubit. The 8910' length would translate to 5184 Egyptian Royal Cubits of 20.625" each or 4320 X 2.0625' (24.75"). Of course, there was the 24750-mile equatorial circumference navigational method, where 1 arc-minute was 6050' or 20.625" X 3520.
The English mile (5280') is 20.625" X 3072 (or 2.0625' X 2560). The Scottish mile* (5940') is 20.625" X 3456 (or 2.0625' X 2880). The English league (16500') is 20.625" X 9600 (or 2.0625' X 8000). The English furlong or furrowlong (660') is 20.625" X 384 (or 2.0625' X 320), etc. The evidence that all ancient increments were in factorable numbers in direct ratio to greater or lesser increments within the same group, shows us that the original Scottish ell measurement was 37.125" (37 & 1/8th). A distance of 24.75' would be 8 ells.
The angle (264-degrees) relates to the English mile of 5280' (2 X 2640). The return angle (84-degrees) was much used in calculations and, in a mathematical progression, generates a string of highly useful navigational numbers. For example, the sum of 840' would be 1/8th of the 6720' Irish mile or 8400' would be 1.25 Irish miles (1 & 1/4th).
(2). From Knowth to Newgrange chambered mound (lower white line) would have carried the codes of 4147.2' @ 124.416-degrees.
In the 24883.2-mile equatorial circumference navigational method, the sum of 4147.2-miles would be 1/6th part or 60-degrees of arc. Likewise, in the 24883.2-mile equatorial circumference, the sum of 12441.6-miles would be 1/2 the distance around the world or 180-degrees of arc.
(3). From Newgrange chambered mound to Dowth chambered mound (red line) would have carried the codes 6336' @ 58.6666-degrees.
Again we see expressions of the Egyptian Royal Cubit @ 20.625". This distance is 2.0625' X 3072. The 6336' distance would be 1/20625th of the 24750'-mile circumference of the Earth (130680000'). It would also be 1.2 miles of 5280'.
The degree angle (58.66666-degrees) is also navigational coding under the English mile system and the sum of 58.66666' (58 & 2/3rds) would be 1/90th of a mile.
(4). From Newgrange chambered mound to Dowth Henge (yellow line) would have carried the codes 9953.28' @ 243-degrees.
In the 24883.2-mile circumference of the Earth, there would be 9953.28-miles X 2.5.
The multi-use value, 243, in a mathematical progression, generates a string of navigational and lunar numbers. The Roman mile was possibly read two ways, but primarily as 4860' , based upon a Roman foot of 11.664". However, for practical overland measurements a foot of 11.6666" was probably used, equating to a simple 11 & 2/3rds inches, whereas the 11.664 foot was excellent as a lunar cycle calculator or in, especially, volume measures in cubic inches.
The sum of 243' would be 1/20th of a Roman mile. The sum of 243-days would be 1/28th of the 6804-day lunar nutation cycle or there would be 10.5 intervals of 243-days in the 2551.5-days (7.2 lunar years) monitored within the lunisolar Sabbatical Calendar (alongside 7-solar years or 2556.75-days).
(5). From Dowth chambered mound to Dowth Henge (blue line) would have carried the codes 3675' @ 70.4 degrees in one of the coded readings (marked by stones at or near the centre crown of Dowth chambered mound). The sum of 36750' would be 7 Greek miles, making this distance .7 of a so-called Greek mile.
The degree angle is related to the 5280' mile, of which 70.4 feet would be 1/75th.
(6). As already shown, the distance and angle from Dowth Henge to the centre of Knowth chambered mound is 12500' (2 & 4/7ths Roman miles using the foot of 11.6666") @ 260-degrees (80-degrees return).
This distance is 1/4th of 50000' and provides a baseline where triangulation calculations could be initiated using decimal values. An enlarged baseline of 12600' (2.4 miles of 5250') would have been very dynamic and useful also.
The 260-degrees angle was in mnemonic reference to the solar year, composed of 26 bi-weeks or 52 weeks of 7-days each. Under the Sabbatical Calendar system there were 13-months of 28-days each in the year or 364-days (1.25-days of error). This small accumulation of annual error was allowed to persist for 7-solar years and, at the close of the Sabbatical Year (7th year), a 9-day festival occurred, where 8.75 intercalary days were added to the calendar and the count started anew with everything corrected.
The 80-degrees return angle highlights counts by 8, 16, 32, 64, 128, 256, 512, etc.
So, we're getting some small idea and appreciation of what Julius Caesar meant when he stated:
'They also lecture on the stars in their motion, the magnitude of the Earth and its divisions ...' (see De Ballo Gallico, VII, 15, 16.).
DOING IT BY THE NUMBERS.
This, Boyne River Valley, far more ancient predecessor to the Druidic schools of Caesar's day, appears to have been a grueling, comprehensive educational environment, where only the brightest and the best would have any chance of completing the navigational course. There were no books, only the perfectly memorised mathematical concepts passing directly from the tutors. Certain of the kerbstones at the base of the giant chambered mounds had pictorial lesson material inscribed into them, but all of the number progressions, their meanings and applications to cyclic astronomy or navigation had to be memorised perfectly by repetition and rote learning, in much the same way as a modern pupil learns his or her times-tables. The cyclic-astronomical and navigational sciences were encoded within number families and factorable number strings, which had to be memorised as whole numbers or fractionated expressions of the same.
Beyond the grueling memory work was the difficult process of actual navigating overland by the coded distances and angles. Under the concept that, if you don't use it you lose it, it was far more useful to keep the special scientific numbers at the forefront of mental concentration and use them, exclusively, in orienteering exercises for distances to cover and angles to follow. This provided hands-on, constant experience with the parcel of special scientific numbers, as well as their profound meaning and interpretation.
Beyond Dowth Henge or Knowth, Newgrange & Dowth chambered mounds, the secondary surveying stations or outer-marker targets (artificial islands) were carefully placed in the surrounding landscape. The idea was to position them in such a way that students navigating from 4 different beginning points could still locate the target objective by traveling on exclusively coded distances and angles.
By very careful pre-planning, an outer satellite target could be positioned with good relative accuracy to meet the code-bearing requirements, sufficient for students to find it from the 4 variable points of departure. The act of being out on a quest for many hours, and using these special numbers to find the objective, would go a long way towards memorising the numbers and their scientific applications.
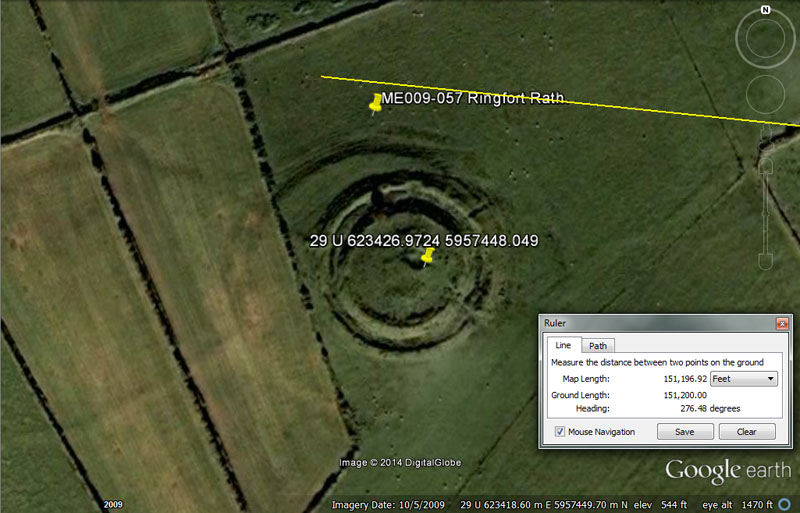
Like Slieve Gullion Mountain in County Armagh, this site at Drumsawry sits 151200' from the centre of Dowth Henge (25 minutes of equatorial arc for the world under a system built into the base dimensions of the Great Pyramid @ 756' per side or 1512' for two sides).
The very impressive ringfort rath sits at a coded angle 276.48-degrees. Under the ancient reading of the Earth's circumference as 24883.2-miles, the sum of 276.48-miles would be 1/90th or 4-degrees of arc.
The fact that this vector, extending overland for 22.5-Irish miles (about 29-miles of 5280') from Dowth Henge, only misses the epicentre of its target by 270', is very remarkable surveying accuracy.
ANOTHER EXAMPLE: MONTFORTESCUE
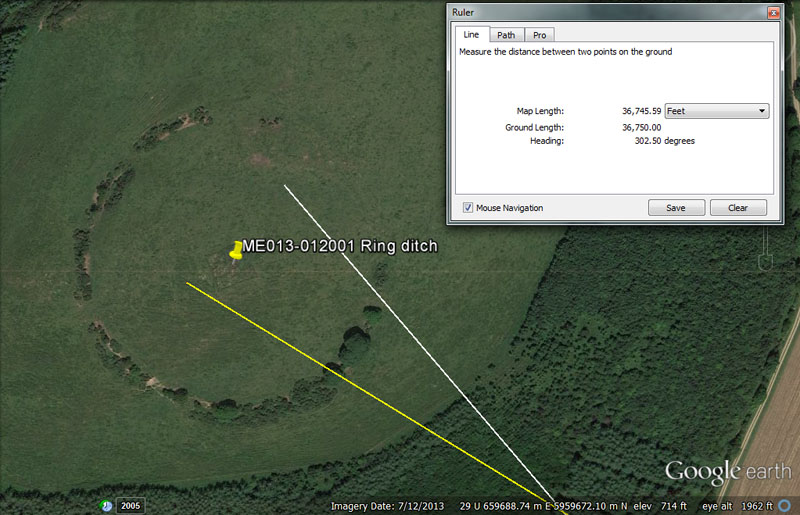
The centre of Mountfortescue ring ditch hill, also referred to as a tumulus and hillfort, sits exactly 7 so-called Greek miles (36750') from the centre of Dowth Henge (yellow line) at an azimuth angle of 302.5-degrees. From Knowth passage mound the distance is 28800' (2 geomancer's miles) @ 320-degrees (white line) for a return angle of 140-degrees.
There are a number of very clever codes built into this position and the near approaches to the circuiting ring were, undoubtedly, once-marked by obelisks or cairns to provide additional distance and angle codes for the students to extract. These would have related to the equatorial size of the Earth under the three main navigational systems in use at that ancient epoch ... one using miles of 5280' (English) & 5940' (Scottish) respectively and another using miles of 5250' (Greek), 6720' (Irish) & 4860' (Roman) respectively.
Also, Mountfortescue's circuiting ringed ditch (a slight oval) appears to provide the same navigational codes as Silbury Hill in Southern England, by way of the two 90-degrees opposed diameters, ditch-centre-to-ditch-centre, in cross measures of the site (550' & 525' respectively).
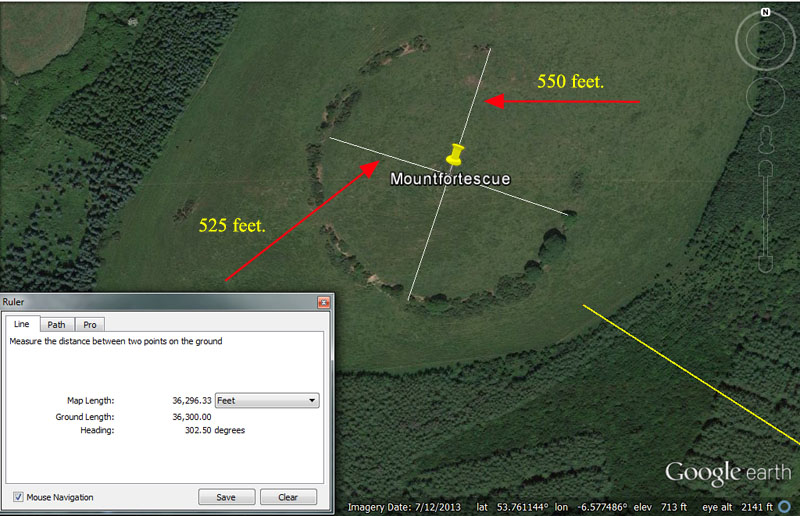
A yellow line, extending from the centre of Dowth Henge is seen to fall just short of the Mountfortescue ring-ditch to resolve at 36300'. At a point 12-feet back from that end point would be a resolving position of 36288'. Both of these values would represent 6-minutes of equatorial arc under two slightly different navigational systems in use at the time, one based upon a mile of 5280' and another based upon a mile of 5250'. Also the degree angle to the centre of Mountfortescue (302.5-degrees) is in mnemonic reference to the same thing (inferring the values 3025 or 3024 and mnemonically referring to 1/2 of 1 minute of equatorial arc under two slightly different navigational systems).
Using for comparative-analysis other well known coded structures found at other sites beyond Ireland, here's how the codes of distance and angle, as well as how they refer to the equatorial size of the Earth, would have been taught to initiates at Dowth Henge - Mountfortescue:
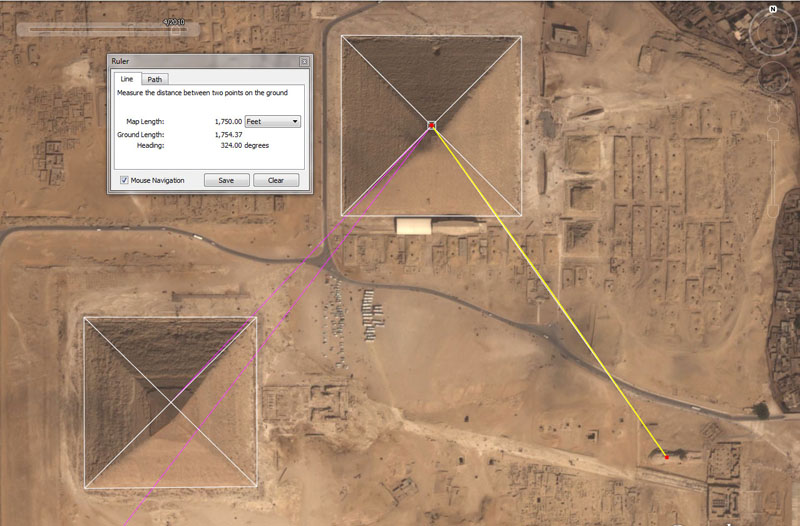
The navigational codes built into the Mountfortescue
Hill ring-ditch position are encoded into the base dimensions of the Great
Pyramid of Egypt (top centre), which is 756' per side or 3024' (36288")
for one circumnavigation. Two circumnavigations = 6048 feet or 1-minute of
equatorial arc for the world (the 5250' mile method) ... culminating in a
world of 12 X 12 X 12 X 12 X1.2 Greek miles.
Similarly, by symbolically elongating the Great Pyramid by a mere 3-inches,
another navigational method comes into play, wherein one circumnavigation =
3025' (36300") and two circumnavigations = 6050' for 1-minute of equatorial
arc (the 5280' mile method) ... culminating in a world of 24750 English miles.
The Khafre Pyramid (Egypt's Pyramid of the Moon) is seen at the bottom left, with side lengths of 708.75' (15/16ths the length of the Great Pyramid) for a total perimeter circuit length of 2835'.
Therefore, Mountfortescue's entryway was coded to be sitting 6-minutes of equatorial arc distant or 1/3600th of the equatorial distance around the Earth under each of the two, marginally different navigational methods.
The slightly oval ditch around Mountfortescue duplicates the base codes built into Silbury Hill in Southern England, wherein one cross measure was 525' and the 90-degrees opposed measure was 550'.
The intended tutorials in each of these cross measures related to doing linear distance legs of travel at sea, dead reckoning and positional plotting.
Method 1:
The sum of 525' is 1/10th of a Greek mile and is also called a short stadia. When sailing a zigzag course at sea (at known degree angles) across a leyline in legs of 5250 feet (or greater and lesser expressions within the same family of increments) at the completion of each leg it was essential to plot the leg on the navigational chart and then work out the angle back to the point of departure or onwards to the destination.
For this it was also essential to turn the 5250' leg traveled into a circumference, using PI @ 22/7.
Therefore 5250 X 22/7 = 16500 (1 English league or 3.125-miles of 5280') ÷ 360 = 550-inches per degree of arc. Using a scale rule and calipers, one could then work out the angle to the destination or back to the point of departure.
Method 2:
The sum of 550' is 100 ancient fathoms of 5.5' each (the merchant navy fathom remained 5.5' into the 20th century) and 960 fathoms = 5280'. The sum of 550' is 1/30th of a league of 16500'
When sailing a zigzag course over a leyline in legs of leagues (or greater or lesser expressions within the same family of increments) the PI value used was 1728/550ths, converting a league of linear distance traveled to a circumference of 51840'* ÷ 360 = 144' per degree of arc.
Again, by use of a scaled rule and calipers accurate angles back to the point of departure or onwards to the destination could be calculated during a zigzag traversal of the ocean when tacking on the wind.
*Note: The distance and angle to Dowth Henge from An Forradh's inner sanctum (the king's seat atop the Hill of Tara from which 142 Irish kings ruled) were coded to be 51840' @ 30.25-degrees.