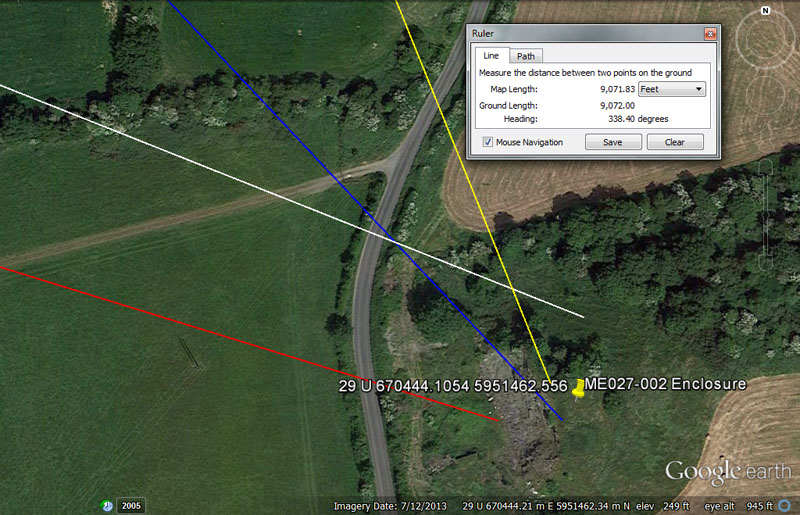
MORE SITES

A large enclosure once sat at this marked position at Cruicerath, which much later became a quarry site millenniums after the Boyne River Valley open-air-university was abandoned and fell into disuse.
From Knowth = 16875’ @ 291.6-degrees.
There would be 21 intervals of 16.875-days (16 & 7/8ths) in the lunar year of 354.375-days. The distance would also be 3 & 3/14ths miles of 5250'.
The degree angle is navigational and 29160' would be 6 so-called Roman miles, 30000 Roman feet or 6000 Roman paces. That same distance would be 1/4480th of the 24883.2-mile (of 5250') equatorial circumference of the Earth.
From Newgrange = 12800’ @ 288-degrees.
The use of the 128 value in the distance is in homage to halving quartering, etc., the Earth into smaller divisions (ie) 1/2, 1/4th, 1/8th, 1/16th, 1/32nd, 1/64th. 1/128th, 1/256th, 1/512nd. A 128th division of the 24883.2-mile circumference would be 194.4-miles.
The 288 value found in the degree angle was multi-use in antiquity for all manner of calculations. There would be 21 increments of 288' in 1-minute of equatorial arc (6048') or 126 increments of 2880' in 1-degree of arc (362880') under the 24883.2-mile assignment. The Egyptian pyramid acre was 28800 square feet. The sum of 28800' was 2 Geomancer's miles. In the 25920-year duration of the Precession of the Equinoxes the sum of 2880 years would be 1/9th of the cycle. In the 24883.2-mile equatorial circumference the sum of 28.8-miles would be 1/864th division, etc.
From Dowth Mound = 9953.28’ @ 316.8-degrees.
This distance is the same as that which runs from the centre of Dowth Henge to the centre of Newgrange chambered mound. In the equatorial circumference of the Earth the sum of 9953.28-miles X 2.5 = 24883.2. The sum of 995328' would be 1/131.25th of the equatorial circumference.
The degree angle is navigational coding and 31680' would be 6 miles of 5280' each.
From Dowth Henge = 9072’ @ 158.4-degrees.
This distance is 1.5-minutes of arc.
The degree angle is also navigational and 15840' would be 3-miles of 5280' each.
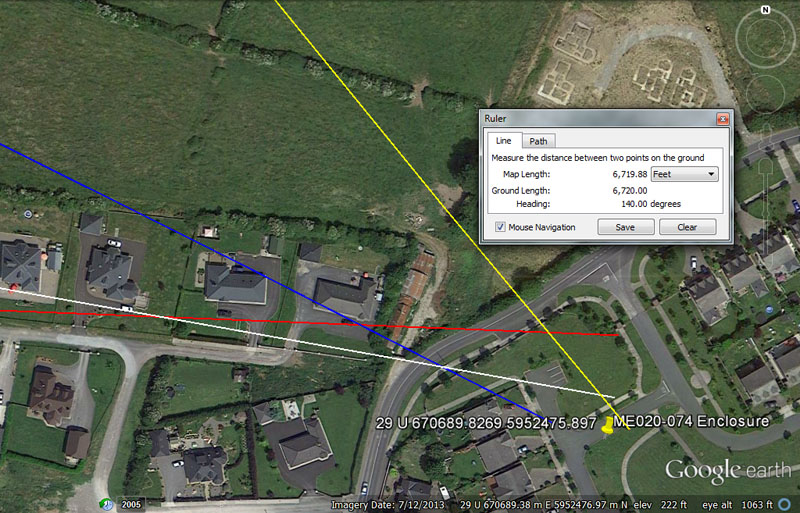
In this suburban setting at Cruicerath was a former large enclosure, which could be found by students issuing forth from the 4 main centres and navigating to the site on the following distances and angles:
From Knowth the distance is 16875’ @ 100-degrees.
Again, use of the lunar code 16875. There would be 21 intervals of 16.875-days (16 & 7/8ths) in the lunar year of 354.375-days. The distance would also be 3 & 3/14ths miles of 5250'.
From Newgrange = 13200’ @ 92.16 – 272.16-degrees.
This distance is 2.5-miles of 5280' each.
The two-way coding of the degree angle is dynamic and 921.6-miles would be 1/27th of the 24883.2-mile equatorial circumference whereas 2721600' would be 1/48th of that distance or 7.5-degrees of arc.
From Dowth Mound = 8640’ @ 297-degrees.
The sum of 8640-years would be 1/3rd of the 25920-year Precession of the Equinoxes cycle and 8640' would be 1/7th of 10-minutes of equatorial arc (60480'). The sun is 864,000-miles wide.
The degree angle is, of course, in homage to the 5940' mile (2970' X 2).
From Dowth Henge = 6720’ @ 140-degrees.
This distance is, of course, recognisable as 1 ancient Irish mile.
The degree angle is self-explanatory as a much used value in calendar calculations, etc.
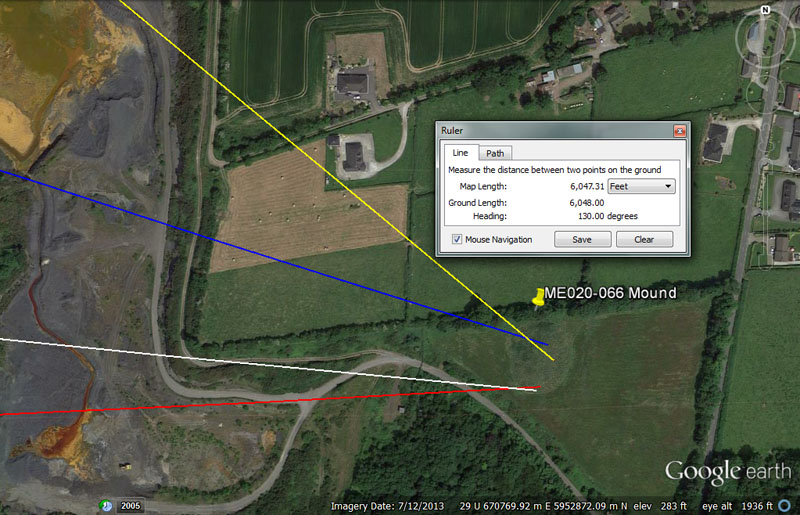
At the townland of Donore (Kells Lower By.) is this enigmatic mound that archaeologists have registered, but remain uncertain about in terms of its status as a monument. The position of this otherwise impressive structure would indicate that it was indeed purpose-built as a code bearing outer-marker to the ancient Boyne River Valley school of navigation.
From Knowth = 17010’ @ 96-degrees.
This distance (3.24-miles of 5250' or 3.5 so-called Roman miles of 4860') is lunar coding and 1701-days would be 1/4th of the 6804-day lunar nutation cycle.
The degree angle is in homage to a multi-functional value, much used in ancient calculations and 960' would be 1/7th of the 6720' in an ancient Irish mile.
From Newgrange = 13440 – 13500 @ 87.5-degrees.
This distance is 2 Irish miles of 6720'. Tutorials related to 13500' could also have been included. The sum of 135-degrees would be 3/8ths of a 360-degree circle.
The degree angle is both navigational and calendar coding and the sum of 875' would be 1/6th of the 5250' mile. There would be a shortfall of 8.75 solar-days at the end of the Sabbatical Calendar cycle and these would need to be added in during a 9-day festival of intercalary days before the next Sabbatical count could start.
From Dowth Mound = 8505’ @ 108-degrees.
Again, the distance is lunar coding and equates to either 1.62-miles of 5250' or 1.75-miles of 4860'. The sum of 850.5-days would be 1/8th of the 6804-day lunar nutation cycle.
The degree angle is in homage to a multi-use number. There would be 24 X 1080-years in the 25920-year Precessional cycle. The sum of 108' would be 1/56th of 1-minute (6048') of equatorial arc, etc.
From Dowth Henge = 5940’ @ 129.6 - 130-degrees (also 6048’).
This distance is, of course, 1 ancient Scottish mile. Over the expanse of the mound it would also have been possible to call the overall distance from Dowth Henge 6048' or 1-minute of equatorial arc.
Over the expanse of the large mound, two coded angle vectors were possible, falling to the northern and southern edges. If called 129.6-degrees, this value would relate to the Precession of the Equinoxes, the half duration of which was 12960-years. If called 130-degrees, the value 13 was important to the Sabbatical Calendar count with 13-months in the year of 28-days each (364-days) and 1.25-days of error allowed to accumulate for 7-solar years until correction during a festival.
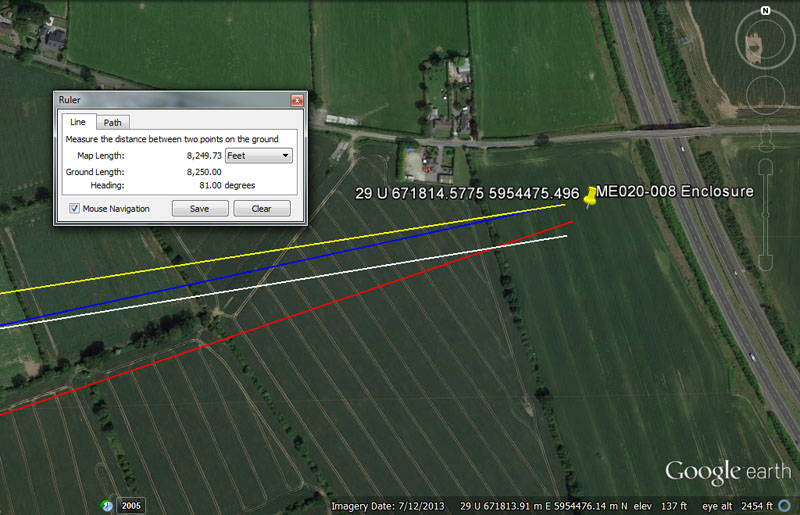
An enclosure, now reduced to nothing but a crop mark, once existed in this Sheephouse field.
From Knowth = 20736’ @ 80.64-degrees.
This distance is 248832 inches, for mnemonic recall of the 24883.2-mile equatorial circumference. It is also 12000 of the largest Egyptian Royal Cubits @ 20.736" (1.728'). A length of 20736' would be 1/6300th of the 24883.2-mile (of 5250') circumference.
The degree angle is navigational coding and the sum of 806400' would be 1/162nd of the equatorial circumference. Likewise, a distance of 80640' would equate to 12 ancient Irish miles of 6720' each. The distance of 6048' (1-minute of equatorial arc under the Greek mile system) is .75 of 8064' (80 arc seconds of 100.8' each).
From Newgrange = 18000’ @ 71.28-degrees.
The distance is self-explanatory.
The degree angle is navigational and 71280' would be 12 Scottish miles of 5940'.
From Dowth Mound = 11880’ @ 77.76-degrees.
The distance of 11880' is 2 Scottish miles of 5940'.
The angle coding is also navigational and 777.6-miles would be 1/32nd of the 24883.2-mile equatorial circumference.
From Dowth Henge = 8250’ @ 81-degrees.
This distance is half a league of 16500'.
The degree angle is also navigational and 810' would be 1/6th of the so-called Roman mile of 4860'.
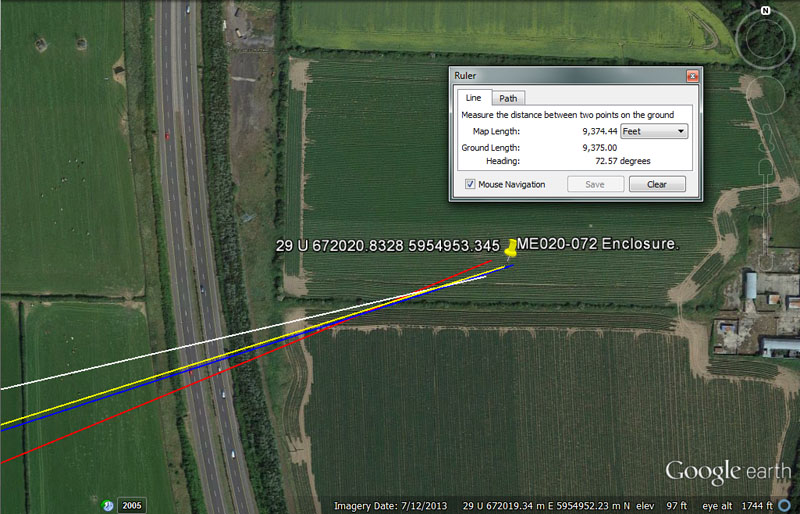
Again, the archaeological register places an enclosure, now reduced to a crop mark, at exactly this position in an Oldbridge field.
From Knowth = 21780’ @ 76.8-degrees.
This distance is 4 & 1/8th miles of 5280'. It would also equate to 1/6000th of the 24750-mile (of 5280') equatorial circumference.
The angle code is navigational also and a distance of 7680' would be 1/17010st of the 130636800' equatorial circumference. Of course, 1701-days would be 1/4th of the lunar nutation cycle. In the 69.12-mile reading for 1-degree of equatorial arc, the sum of 7.68-miles would be 1/9th part.
From Newgrange = 19250’ to 19440' @ 67.5-degrees.
This distance would equate to 3500 ancient fathoms of 5.5' each. However, the intended code, which would overshoot slightly, was probably 19440' or 1/6720th of the 24883.2-mile equatorial circumference. The sum of 194.4-miles would be 1/128th of the 24883.2-mile circumference.
The degree angle relates to the 360-degree compass divided up into 1/16th divisions, in which 67.5-degrees would be 3/16ths.
From Dowth Mound = 13068’ @ 72-degrees.
This distance would be 1/10000th of the 24750-mile (of 5280') equatorial circumference. In the same vein, this distance is 2.475-miles.
From Dowth Henge = 9331.2’ @ 72.576-degrees.
The sum of 93312' would equate to 1/1400th of the 24882.2-mile equatorial circumference. The Sumerian-Babylonian Heavy Talent weight was 933120-grains and 933120' would equate to 192 Roman miles of 4860' each.
The degree angle code is navigational also and, in the 24883.2-mile (of 5250') circumference (130636800') 1-degree of arc would be 362880'. The sum of 72576' would be 1/5th of 1-degree of arc or 12-minutes of arc.
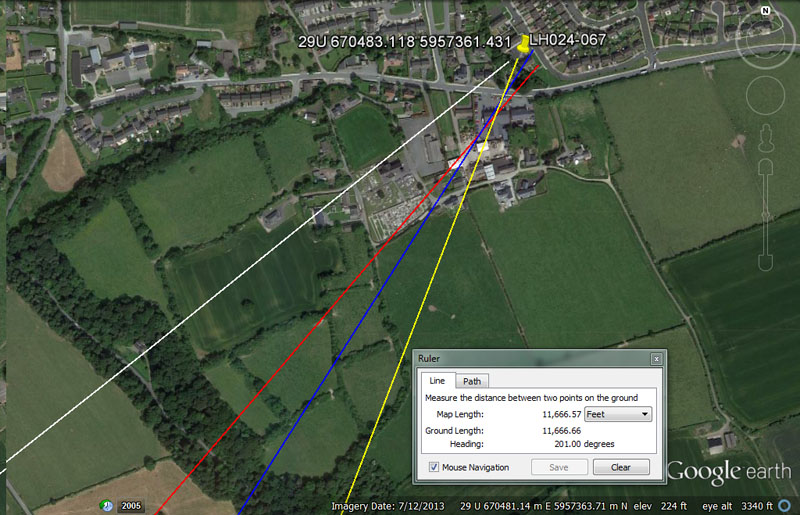
We'll finish up our sampling of ancient structures, around-&-away from the 4-main centres of the Boyne River Valley, with this former enclosure at Tullyallen.
From Knowth = 20160’ or 21000’ @ 51.5625-degrees.
This distance could be read as either 3 & 1/3rd minutes of equatorial arc, 3 Irish miles or 4-miles of 5250'.
The sum of 51.5625' (51 & 9/16ths) would be 30 Egyptian Royal Cubits of 20.625" (20 & 5/8ths). In the 24750-mile reading of the Earth's equatorial circumference, the sum of 515.625-miles would be 1/48th part or 7.5-degrees of arc.
From Newgrange = 20250 @ 40.5-degrees.
The length and angle values mirror each other and twice 20250 = 40500. These are both, primarily, lunar codes and in the 6804-day lunar nutation cycle there would be 40.5 intervals of 168-days. Likewise, in the 2551.5-days (7.2 lunar years) monitored alongside 2556.75-days (7 solar years) in the Sabbatical Calendar count, there would be 63 intervals of 40.5-days
From Dowth Mound = 14400 @ 32.4-degrees.
This distance is 1 Geomancer's mile.
The 324 value was highly important to many kinds of navigational and cyclic astronomical calculations and 3240-years would equate to 1/8th of the duration of the Precession of the Equinoxes (25920-years). Likewise the sum of 32.4-miles would be 1/768th of the 24883.2-mile equatorial circumference.
From Dowth Henge = 11664’ @ 21-degrees.
This distance is 2.4 so-called Roman miles. The Roman foot was 11.664". The Egyptian Theban volume was 11664 cubic inches, whereas their Besha was 1166.4 cu" and Honnu 116.64 cu".
The degree angle is self-explanatory, but a distance of 21000' would be 4 so-called Greek miles of 5250'.
JULIUS CAESAR KNEW WHAT HE WAS TALKING ABOUT IN RELATION TO THE GREAT DRUIDIC SCHOOLS.
Historian, Isabel Hill Elder paraphrased the words of Julius Caesar, stating that the Druidic schools of Great Britain, in the BC era, were teaching about: the stars in their motion, the magnitude of the Earth and its divisions ... astronomy, mathematics, geometry ... with severe exactitude.
Of course, they taught many other subjects as well, and we have only touched upon some of the navigational and astronomical tutorials being learnt by hands-on experience, rote-learning and grueling memorisation. Students had to walk-the-walk & talk-the-talk for years in order to become adept in the navigational arts.
One needs to reflect upon the question:
By what methods could world-traversing navigation have been taught in circa 3000 BC, in an age where very perishable paper was a luxury and text books or scrolls were all but unavailable?
The answer is found in setting up a system of carefully placed, distantly scattered, artificial islands away from hub positions and then devising imaginary labyrinth or maze puzzles between selected groupings of these islands Students would then be required to find their way around the maze using only landmarks, the sun, moon, planets and bright stars or zodiacal constellations as the solitary guideposts.
It was highly important to be able to judge distances and to constantly do it by the numbers. A large parcel of scientific numbers, their mathematical progressions and fractionated expressions, related to the size of the Earth and its divisions, cyclic-astronomy and the lunisolar calendar, had to be indelibly affixed into memory, never to be forgotten.
There was no point in using arbitrary or meaningless numbers during these forays out-&-about across the landscape, only scientific ones from a special parcel handed down by ancestor-savants. These hard-won values, the numbers of civilisation, abundance and order, were incorporated into all weights, measures and volumes standards, such that they would never be lost.
The same numbers and standards or ratio-related expressions of the same, were used by all of the great Mediterranean and Continental European - British Isles civilisations from remote antiquity.
So now that we've established that these first-objective, outer-stations could be reached by a coded distance and angle, let's assign a novice group an erratic, zigzag journey around a selection of artificial islands, doing it by the numbers. In truth, there were so many scientific numbers to choose from, either as whole numbers or broken down into fractionated form, that assigning navigational tasks over limited lengths, posed no problem:
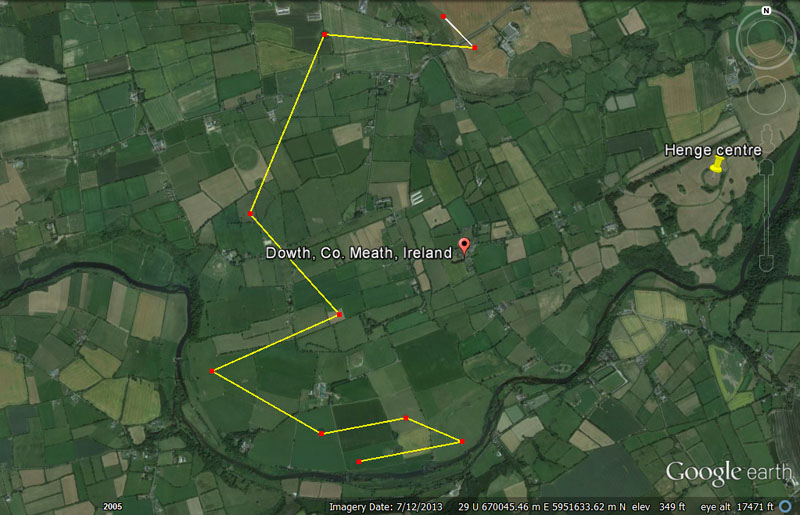
A small group of students from Newgrange chambered mound head due South at first light and congregate at a large enclosure near the Boyne River. They measure the site and work out its diameter and circumference codes. They then move on to their next objectives, which include:
1. A journey of 2640' @ 79.2-degrees to a round mound.
2. A journey of 1536' @ 113.4-degrees return to a square mound sitting at an offset angle.
3. A journey of 2160' @ 259.2-degrees to a pond barrow.
4. A journey of 3168' @ 120-degrees return to an enclosure.
5. A journey of 3500' @ 66-degrees to a ringfort rath.
6. A journey of 3402' @ 138.24-degrees return to another enclosure.
7. A journey of 4860' @ 22.5-degrees to a pond barrow.
8. A journey of 3780' @ 275-degrees return to a perfectly circular ring ditch.
9. A journey of 1100' @ 315-degrees to locate their souterrain accommodation for the night.
On the morrow they will navigate to yet more objectives, recording the site attributes and type, as well as extracting in-built codes of diameter and circumference.
With over 1800 such sites in County Meath alone, approachable from any direction or able to be randomly selected to form varied orienteering courses for dawn-till-dusk exercises, there were enough sites to keep the student navigators busy and on-the-job or absorbed in their training for years.