Lothrop writes:

'This is an oval mound located just north of site F. On top there are four stone balls of moderate size. Three of these are in a line on the main axis of the mound and the fourth is placed off centre to form a triangle (fig. 6). We did no digging in this vicinity'.

STONE SPHERE A

Lothrop gives 90-degrees opposed diameters to this stone and shows it to be quite irregular, with diameters that varied by 3 & 3/20ths -inches. The overall circumference, however, sits very close to a dynamic code to do with the equatorial circumference of the Earth. Perhaps it was used to demonstrate 6.2208-feet. There would be 4000 X 6.2208-miles in the 24883.2-mile equatorial circumference and 6220.8-miles was quarter of the circumference.

STONE SPHERE B

All of the stones in this lineup are very close in overall diameter and this one produces a circumference of 6.804-feet, which is a dynamic code related to the duration of the lunar nutation cycle (6804-days).

STONE SPHERE C

The circumference of this stone falls very close to 6.3-feet (with a shortfall of about 1/7th of an inch). The probable circumference code was 6.3-feet, which is 75.6-inches or 6 Greek feet. The side length of the Great Pyramid was 756-feet and this value was 1/8th of 1-minute of equatorial arc.

STONE SPHERE D

The circumference of this stone was 6.48 to a shortfall of 1/5th of an inch. This value (77.76-inches) would be a very dynamic navigational code and there would be 32 X 777.6-miles in the 24883.2-mile equatorial circumference.

STONE SPHERE E

Lothrop's recorded circumference for this stone sits close to 6.4-feet, to a shortfall of about 3/7ths of an inch. In the Sabbatical Calendar counting system the values of 63 & 64 were used side by side to calculate the lunar period alongside the solar period. Stone sphere C seems to infer 6.3-feet and stone sphere E seems to infer 6.4-feet. For further insights go to: The Calendar of Coligny

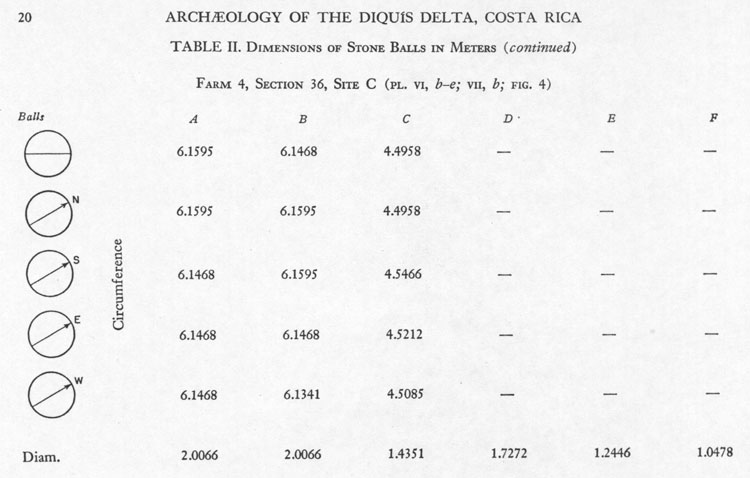
FARM 4 SECTION 36 C

In this section Lothrop encountered some very large stone balls.

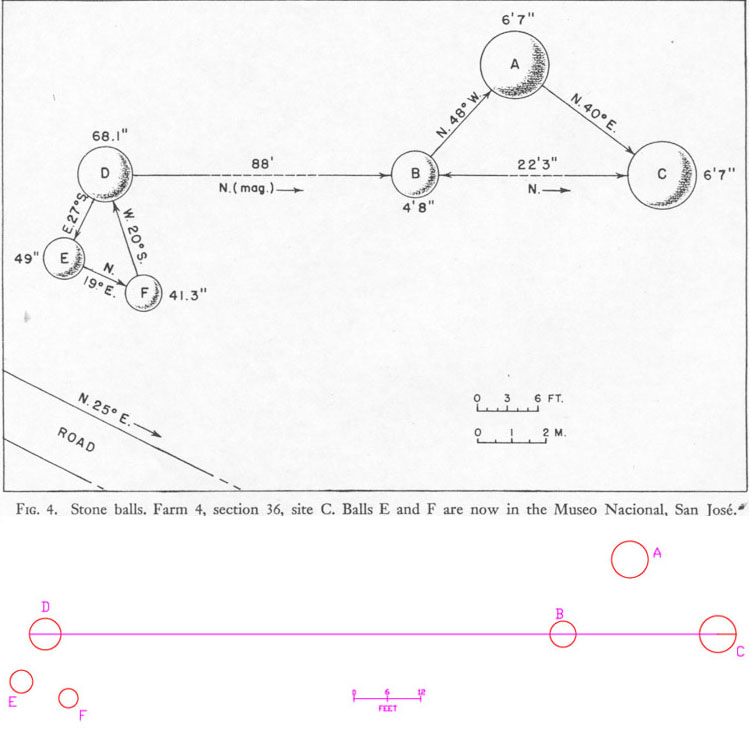
Apart from Lothrop's list of exhaustive diameter measurements of each individual stone ball, he includes a drawing showing the entire alignment layout, as well as the distances and angles between component stones. Although some distances are not listed, that aspect can be calculated by trigonometry, based upon the angle information supplied. The colour drawing attached to the bottom of the black & white one appearing in Lothrop's report was made in AutoCAD architectural program and is scaled according to Lothrop's recorded dimensional and angular determinations.

In the following analysis we will use Lothrop's measured diameters, as found in the drawing. Eleanor Lothrop, who was one of several participants helping her husband measure the stones, describes the process in very entertaining fashion:

'On the morning we started work, I was surprised to see that Sam’s equipment consisted of a tape measure and a fishing line with a lead sinker hanging from the end of it. “Where’s your hook?” I asked, wondering if he had decided to have a day’s fishing on the near-by river.
He gave me a long-suffering look. “This is a plumb bob,” he explained. “It is attached to what is called a plumb line.” He spoke slowly and clearly as if to a child. “As the bottom of many of the big balls are underground, and it would take too long to dig them out, we will use the plumb bob to measure their diameters to find out if the balls are perfectly round. See?”
“Of course,” I said at once, although I didn’t see at all.
I still don’t see, although for many days I watched Sam performing incredible gyrations with plumb line dangling from one hand and tape measure clutched in the other, while I ran around blindly jotting down figures.
The first site we tackled contained three enormous stone balls, and after several hours of mysterious computations, Sam pronounced all three to be six feet in diameter and practically perfect spheres.
“Good,” I said with relief, as the temperature had reached 94 degrees and my head ached. “Let’s go home and have a cold drink.”
“Not at all,” said Sam. “As long as the diameters don’t show any variation, we’d better take the circumferences.”
“Why?” I asked, which is the word I use most frequently on archaeological trips.
Sam sighed. “Because anything that is six feet in diameter must be almost twenty feet in circumference, and errors will therefore be more easily detected.”
This time I swallowed the “why” because I recognized that no explanation would make a mathematician of me. So we enlisted the aid of two workmen to help hold the tape.
Even so, it was a difficult job. We took five circumferences on each of the first two balls. Sometimes I would climb on top of the sphere, sometimes lie on the ground, and occasionally I tried to stand on my head. When the measurements all turned out to vary less than an inch, I decided we had done an awful lot of work for nothing; but Sam seemed pleased' (See Natural History, September 1955).

Left: Stone balls and a statue removed from the vicinity or atop the mounds where they sat "in situ" to become garden ornaments at the home of the farm manager. Right: The Lothrop's and one of the farm workers excavating stone balls. It is gratifying to see that Samuel Lothrop was using a theodolite (on tripod) for making his angle determinations. He could, therefore, set the instrument's calibrated disk to north, then shoot all subsequent angles with excellent accuracy and at a standard of precision acceptable to surveyors.

MAGNETIC VARIATION (DECLINATION).

In the course of making his map plans of the Diquis Delta archaeological sites, Samuel Lothrop used a magnetic compass, in conjunction with his optical theodolite instrument, and indicates on his map plans that the directional arrow is pointing to magnetic north. Unfortunately magnetic north is not true north and, depending on where one is on the globe, the error can be substantial, as there is tremendous variation from country to country and from year to year.

Strangely enough, however, Lothrop's magnetic north orientation complied very favorably with the way some stone ball alignments ran, which could cause some researchers to speculate that the ancient astronomer-navigators in Costa Rica were using magnetic compasses to lay out their alignments. What should, conceivably, be pointing to true north was pointing towards magnetic north ... how very bizarre!
The anomaly is explained by the fact that, in Costa Rica, there is almost no difference between true north and magnetic north. It is one of the few locations in the world where this is the case. The evidence suggests that the main, central line of Lothrop's map plan drawing shown above sits on a true north-south orientation and was carefully set out that way by its original design architects.

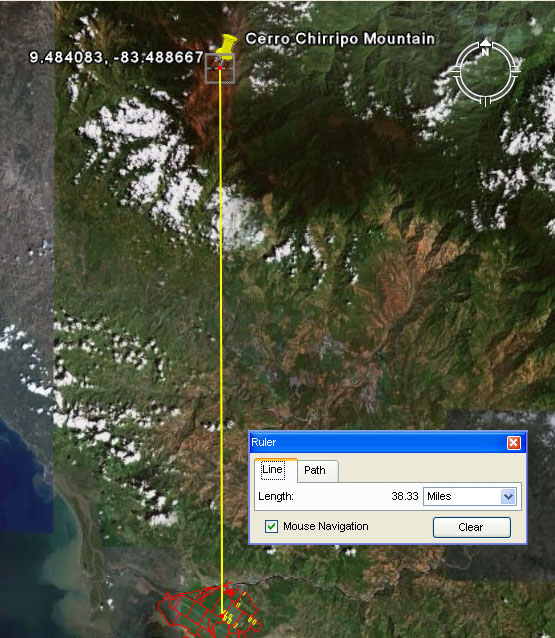
Very compelling evidence to show that the alignment extending from Farm 4, Section 36C points to true north is provided by the above picture. The yellow line runs for 38.33-miles from Section 36 in Farm 4 to the highest spot in Costa Rica at Cerro Chirripo Mountain. The azimuth orientation is a perfect 360-degrees or "True North". From this we can surmise with considerable confidence that the Stone Ball marked as "C" in Lothrop's plan was the primary benchmark position or surveyor's hubstone for the entire stone ball complex within the Diquis Delta. This conclusion is further supported by the sheer size of this stone and its companion stone adjacent (Stone Ball "A"), which shared exactly the same design dimensions.

A surveyor requires a "benchmark" or ground zero position from which all secondary positions are fixed. This position on Farm 4, Section 36 constituted the perfect benchmark position inasmuch as the high point of Cerro Chirripo Mountain acted as the "outer-marker" position that gave a permanent fix on true north. Once this alignment was built, many secondary alignments could be created further afield and even several miles away. Each distance and angle to these secondary groupings (made up of mounds upon which statues and stone balls sat) would be carefully coded to teach a navigational or cyclic astronomical principle.

The student, once having extracted and learnt the multiple codes offered on this site due south of Cerro Chirripo Mountain, could accurately fix onto secondary sites nearby. Using the outer marker target of Cerro Chirripo, an accurate degree angle calculation to any secondary site within view could be identified. The tutor could then ask the students to elaborate upon the significance of the numerical value identified within the degree angle and, if the apprentice navigators were unable to do so, the tutor could teach them the new principle.
Also, this stone alignment at Farm 4, Section 36C was of known measurable length and represented a "surveyor's baseline". By taking an angle fix to a secondary site from the hubstone, then taking a slightly varied fix onto the same target from the other end of the baseline, the student had all of the information necessary to do an accurate trigonometric calculation related to the exact distance away the secondary site target sat from the hubstone. The SINE value number required to calculate the distance could be recorded upon a "quippu" string knot device.

Having learnt the tutorials of this site, students could then move from marker-mound to marker-mound, undertaking calculations as they went and, thereby, learn the skills of navigation that they would need later as navigators aboard ship. They could fix onto any of the high points of the mountain ranges extending in an arc from East to Northwest, including such targets as Cerro Fabrega at 72.6-degrees azimuth from the primary hubstone, etc.

STONE SPHERE A

Lothrop gives a diameter reading for this stone as 79-inches. The encoded value was, in fact, 79.2-inches and contained tutorials related to the diameter and equatorial circumference of the Earth. The literal equatorial diameter of the Earth is 7920-miles to a tolerance of about 6.5-miles. The equatorial diameter of 7920-miles enlarges to 24883.2-miles (12 X 12 X 12 X 12 X1.2) using PI @ 3.141818182 (314 & 2/11ths ÷ 100). Two further Earth diameters, from the main navigational systems would have been automatically inferred by this stone ball's width ...

• 24741.818181818-miles ÷ PI @ 3.141818182 = 7875-miles of diameter.
• 24750-miles ÷ PI @ 22/7 (3.142857143) = 7875-miles of diameter.

STONE SPHERE B

Lothrop gives a diameter reading for this ball as 56-inches wide. The value (7 X 8) was very useful in all manner of navigational and lunar calculations and a mathematical progression, based upon 56 produced much sought after values. There were 56 posts on the Aubrey Circle at Stonehenge over which azimuth calculations, related to the alighting and ascending positions of stars were undertaken and lunar counts within the calendar system were done.

The main attribute of this value to navigators is found in the way that it converts to a circumference using PI @ 22/7. Therefore: 56 X 3.142857143 = 176. It will be recalled that the British mile of 5280-feet is 1760-yards or, alternatively, 1760-feet would be 1/3rd of a mile. The value 56 is a nice ratioed down value of the Greek mile @ 5250-feet.

There was an ancient interplay between the values 55 & 56. Whereas 55 X P1 @ 3.141818182 = 172.8 (a cubic foot = 12 X 12 X 12 cubic inches or 1728), 56 X 22/7 = 176.0. In other words, an "11" based number converts to, essentially, a sexigesimal number and a "7" based value converts to an "11" value using a slightly different rendition of PI. These two mathematical "windows of opportunity" were much exploited by ancient navigators, converting linear distances of travel into circumferences from which positional plotting angles could be accurately determined. The same tutorial was built into the 90-degrees opposed dimensions of the "Crosshouse of Miringa te Kakara", an ancient pre-Maori temple in New Zealand.

STONE SPHERE C

Strangely enough, stone sphere C in the drawing appears to hold exactly the same design coding as stone sphere A. Perhaps there was a subtle difference in diameters that Lothrop did not detect, and each related precisely to one of the two main systems of navigation.

STONE SPHERE D

Lothrop gives a diameter for this stone as just slightly in excess of 68-inches. The actual intended code was 68.04-inches and the coding related to the lunar nutation cycle of 6804-days. It was imperative for the navigator to be able to calculate the moon's position relative to the Earth throughout every day of this long cycle, season by season, as the moon and the gravitational tug it has on our atmosphere is the greatest single determinant of weather conditions. The ancient French artefact called the Calendar of Coligny is capable of calculating the daily lunar position throughout the entire 6804-day cycle.

Using the rendition of PI @ 3.125 turns this diameter into a calibrated circumference (212.625) in which very important lunar intervals can be read. The number produced would, in days, be 1/32nd of the 6804-day lunar nutation cycle. The mathematical progression stemming from 212.625 delivers up many crucial lunar numbers, including 2551.5-days (7.2-lunar years) which was read alongside 2556.75-days (7 solar years) in the age-old lunisolar Sabbatical Calendar.

Ancient Americans fabricated many different disks with calibrated circumferences, depending upon the kind of navigational or cyclic computation they wished to undertake. Here are a few examples taken from the North American mounds, which artefacts probably date to around 3000 BC.

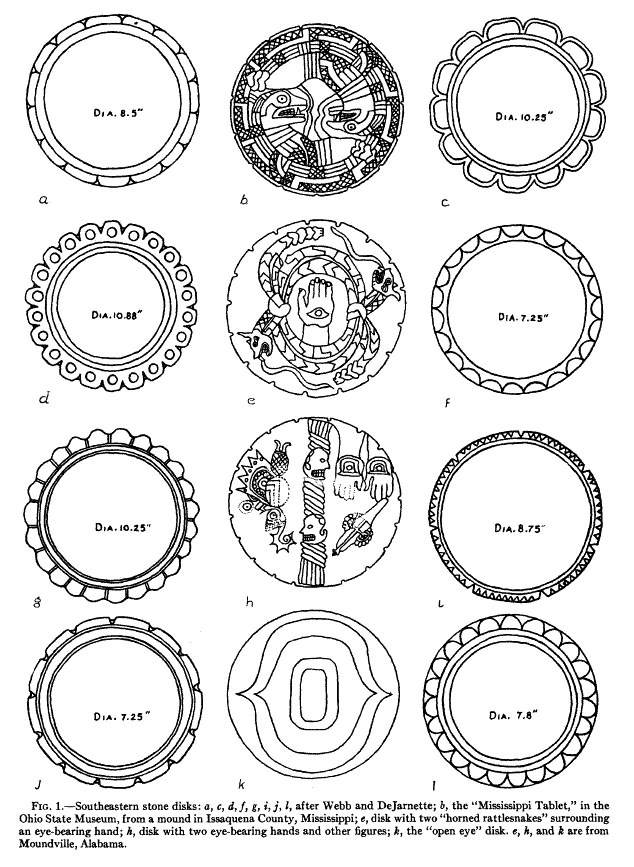
Vol. XII, American Antiquity, July 1946, No 1, pg. 9, Article title: Stone Disks As Treaty Suns. As an example of usage, disk e has 17 calibration segments on the outer rim. One quarter of the 6804-day lunar nutation cycle is 1701-days and this value recurs constantly in ancient edifice measurements. For example: The Khafre Pyramid of Egypt @ 708.75-feet per side (15/16ths the length of the Great Pyramid) has a perimeter value of 2835-feet or 34020-inches. Therefore: 2 side values in inches comes to 17010. It's interesting to note that the hand design on the disk is reminiscent of the "Eye of Horus" from Egypt. The same disk also shows dual snakes, in the same way as ancient Scandinavian monument stones, the Mediterranean Caduceus symbol, the dual snakes (or snake and Ibis bird) on the funerary mask of Egypt's Tutankhamen or at British megalithic sites like Mt. Pleasant.

STONE SPHERE E

Lothrop gives a diameter measurement of 49-inches for this stone ball. The value, undoubtedly, 49 & 7/32nds, as this would be a strong lunar number. The period of 49 & 7/32nds days would be 1& 2/3rds lunar months or 1181.25-hours. Note: 118.125-days would be 4 lunar months. This value, multiplied by PI @ 22/7ths converts to a navigational progression, which reads the Earth's equatorial circumference as 24750-miles. Therefore: 49.21875 (49 & 7/32nds) X PI @ 22/7 = 154.6875 (154 & 11/16ths). The sum of 154.6875-miles would be 1/160th of the equatorial circumference under this system.

The same approach can be used to get a 160th reading of the equatorial circumference, based upon the literal system of the Great Pyramid (24741.8181818-miles). For that calculation, however, PI @ 3.141818182 is used.

STONE SPHERE F

Lothrop gave a value of 41.3-inches for this ball's diameter. It was, undoubtedly, intended to convey 41.25-inches or 1/20th of an inch less than Lothrop's value. The diameter is navigational under the "11" family of numbers and the value of 41.25 sets up a very important mathematical progression related to the 24750-mile equatorial circumference. The sum of 4125-miles would be 1/6th of the size of the Earth under that system. The half value of 41.25-inches is 20.625 and this was the length of the "11" family Egyptian Royal Cubit. Using PI @ 3.141818182, this converts to a circumference of 129.6-inches, which is a Precession of the Equinoxes astronomical value. Precession was calculated to endure for 25920-years (360 X 72) and the half period for Precession was 12960-years.

If we considered the stone Sphere to be two Egyptian Royal Cubits of 20.61818182-inches (the same size as the one on display at the Turin Museum) then that would equate to 41.236363636-inches. This value multiplied by PI @ 22/7ths = 129.6.

We see from this that the stones comply to much used old world numbers. For example:

To get the "6&7" family Egyptian Royal Cubit, simply divide the side length of the Great Pyramid by 440. Therefore, 756-feet (9072-inches) ÷ 440 = 1.718181818-feet (20.618181818-inches).

To get the "11" family Egyptian Royal Cubit, simply divide the symbolically elongated side length of the Great Pyramid by 440. Therefore, 756.25-feet (9075-inches) ÷ 440 = 1.718175-feet (20.625-inches).

Under the ancient Sumerian-Babylonian weights standard a Shekel was 129.6 grains.

THE CODES OF DISTANCE & ANGLE BETWEEN STONE BALLS IN THIS ALIGNMENT.

The three balls on the centre line orientated towards Cerro Chirripo Mountain, situated due north at 360-degrees azimuth. From the southern side extremity of stone sphere "C" of Lothrop's drawing (the hubstone or benchmark position for the entire complex) the accumulating distance up the line is (in inches) 79 + 267 + 56 + 1056 + 68. Let's go step by step up the line and see what the student navigators were learning:

• The 79-inch diameter of "C" related to the diameter of the Earth.
  
  
• The next interval between stones (22-feet, 3-inches or 267-inches) would have been read symbolically as both 266.6666666-inches (266 & 2/3rds) in some tutorials and 266.6 in others. Therefore: 79 + 266.6 = 345.6-inches. The outer rim circumference of the Sarsen Circle at Stonehenge was intended to convey 345.6-feet (11.52-feet X 30 lintel faces). This is a dynamic navigational code and 72 X 345.6-miles would equal the 24883.2-mile equatorial circumference.
  
  
• The merits of the next stone sphere (B) diameter @ 56-inches have been explained. Measuring from its centre back to the face of Stone Sphere C would be 295-inches, which would have been read as meaning 295.3125 (a lunar month is 29.53125-days). Beyond Stone Sphere B is an interval of 88-feet or 1056-inches to the face of Stone Sphere D. This distance would be 1/60th of a mile of 5280-feet.
  
  
• By adding stone sphere B's diameter and the 1056-inches to the earlier length already discussed, the combined total = 1458-inches or 121.5-feet. This distance is 125 Roman feet of 11.664-inches. This was a special "lunar" foot and their overland foot was 11.66666-inches. The distance of 121.5-feet is very dynamic lunar and navigational coding simultaneously and this stretch between the southern end of stone "C" and the southern end of Stone "D" would have worked effectively as a sufficiently long surveyor's baseline for tutorials in trigonometry and the computation of overland distances to other nearby purpose-built mounds.

CODES OF PLACEMENT IN STONE SPHERES "A", "E" & "F".

• Stone Sphere A in Lothrop's drawing, sat an intended 249-inches from Stone Sphere C. Both stones were coding the 24883.2-mile equatorial circumference and this same code was expressed in their centre to centre distance from each other (read as 248.832-inches). Their face to face distance from each other would have been read as 170.1 inches, which is a strong lunar code.
  
  
• Stone Sphere A sat an intended centre to centre distance of 216-inches (Precession of the Equinoxes and Zodiac code) from Stone Sphere B. The face to face separation distance was intended to convey 148.5-inches, which is a navigational code.
  
  
• Stone Sphere D sat an intended centre to centre distance of 146.6666-inches (147) from Stone Sphere F. This is a strong navigational value. The distance would also have been read as 14 & 49/64ths and, in days, that value would be half a lunar month. The face to face separation would have been read as 92.16-inches, which is a navigational code.
  
  
• Stone Sphere D sat an intended centre to centre distance of 115.2-inches from Stone Sphere E and this is a very strong lunar code. The length of the Sarsen Circle lintels at stonehenge would have averaged 11.52-feet in length each for a combined circumference of 345.6-feet. The face to face distance between the stones was 56.7-inches, which is very strong lunar coding.
  
  
• Stone Sphere D sat an intended centre to centre distance of 108-inches from Stone Sphere E and this is a strong navigational code. The face to face reading was 62.5-inches, also a strong navigational code.

DEGREE ANGLE CODES

• "A" to "C" = 40-degrees ... In tutorials this would also have been interpreted as 40.5-degrees and relate very strongly to both navigation and periods within the lunar cycle and Sabbatical Calendar system.
  
  
• "A" to "B" = 132-degrees ... This value was navigational and 1320-feet would be 1/4 of a mile of 5280-feet.
  
  
• "D" to "E" = 117-degrees ... In tutorials this would have been read as 116.64-degrees and 116.66666-degrees respectively. The 116.64 is lunar coding and is also used as 11.664-inches to describe the Roman foot. The Egyptian "Theban" volume was 11664-cubic inches. The Roman Pace is considered to be 58.32-inches, (5-Roman feet) but for overland measurements was 58.33333-inches (5 overland feet of 11.66666-inches each).
  
  
• "D" to "F" = 70-degrees. In tutorials this would also have been read as 70.4-degrees, which is a strong navigational code. The distance of 70.4-feet would be 1/75th of a mile of 5280-feet.
  
  
• "E" to "F" = 19-degrees. In tutorials this would have been considered to be 19.2-degrees, which is strong navigational coding.

Continue