FARM 1, SECTION 29.
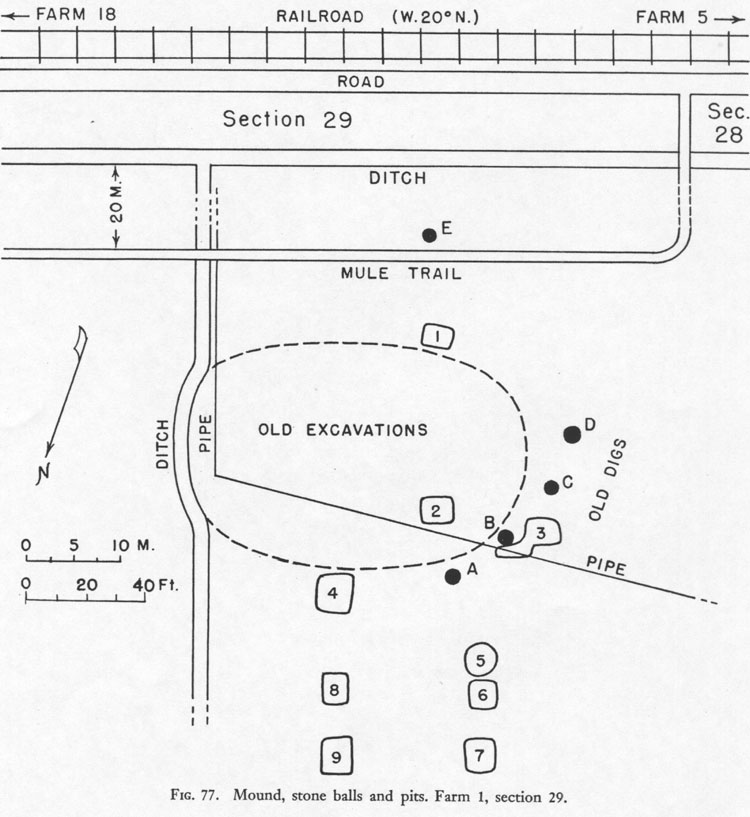
The 5 black dots listed as A, B, C, D, & E, are
stone balls seen and measured by Lothrop and Stone in 1948.
Lothrop writes:
'The principal feature was a mound measuring ca. 35
X 25 by 2 meters (115 X 85 X 6 1/2 feet). It was so big and massive that,
instead of leveling it by bulldozer, a drainage ditch had been curved around
its base (fig. 77).
There were five stone balls, one to the south of and four to the northwest.
In spite of the fact that the latter are almost in line, we believe that all
once had been placed on the mound and had been rolled to their present position,
either purposely or as the result of failure of the retaining walls. Ball
B (pl. VII, d) had the finest finish of any we observed and ranked at the
top for rotundity (table II).'
Here are Lothrop's circumference measurements (in metres) and
calculated estimations of diameters based upon circumferences.

In order to read the navigational coding built into the diameters
and circumferences of these stone spheres, the dimensions have to be converted
back to "inches".
The British standard "inch"
is not British at all, but represents the base increment shared by all of
the Mediterranean and European cousin nations of remote antiquity for their
"feet" or "cubits". Thus, an ancient Greek foot was 12.6-inches;
a Hebrew Reed was 126-inches;
an Assyrian "cubit" was two Greek feet or 25.2-inches,
etc., etc.
Our western systems of chronology (the measurement of time as per 24-hours
in a day, reducing to hours of sixty minutes and minutes of sixty seconds)
or our method of measuring degree angles (as per 360-degrees, reducing to
minutes and seconds of arc) have a direct pedigree back the very ancient Sumerian-Babylonian
system.
At the same time, our measurement systems came from exactly the same source
and all ancient cousin European nations shared the same integrated mathematical
parcel, which was at the foundation of all their weights,
measures, volumes, areas, degree-angles, chronology or calendar standards
and astronomical sciences. Although different sizes or capacities
of national preference existed between the cousin nations, all standards were
in perfect "ratio" to each other and a simple calculation could
convert one national standard for, say, a "talent"of
weight or a "bushel"
of capacity to another cousin nation's marketplace standard.
STONE SPHERE "A"
The measured circumference of this stone sphere converts fluidly
to very slightly in excess of 9.54-feet and the stone contains an important
navigational tutorial based upon 1/6th of 1-degree of arc for the equatorial
circumference of the Earth.
To understand why it was essential to create so many perfectly
(or near perfectly) round stones, one has to appreciate the difficulties encountered
in ancient navigation at sea. It's all to do with linear distances traveled
(diameters) being converted into circumferences. The linear distances for
each leg of travel at sea placed the boat at constantly renewed positions
as the voyage continued and forward progress was made. The circumference calculation
that followed the completion of each "leg" and the beginning of
a new one, told the navigator exactly where on the vast, featureless ocean
the boat sat, as well as the degree angles to point of departure or destination
(this is called positional plotting). Because the ancient mariners used sailing
ships, fully at the mercy of the wind, each voyage was a series of staggered
"tacks" on the available wind. It was imperative that the navigator
stay fully informed about the boat's exact position, either on first-time
exploratory missions or repetitive voyages back and forth to known destinations,
as any dereliction of duty in this regard could spell disaster for the ship,
its crew and precious cargo.
Before any "positional plotting" was possible, the
size of the Earth had to be known with good relative accuracy and a mathematical
system had to exist for grid referencing the Earth into latitude and longitude
sectors. The apparent function of Stone Sphere A, Farm 1, Section
29, was to provide a tutorial in this regard. Here's how it worked:
-
The Great Pyramid of Egypt , in its literal base and height
dimensions, provides an understanding of the size of the Earth, as well
as three systems, using separate number families, of how to grid reference
the Earth for safe and accurate traversals. The literal design length of
the Great Pyramid was 756-feet, which equated to 720-Greek feet, 360 Assyrian
cubits, 72 Hebrew Reeds, etc. Two circumnavigations of the Great Pyramid
was 6048-feet and this represented 1-minute of Earth equatorial arc in a
world that was 12 X 12 X 12 X 12 X 1.2 Greek miles of 5250-feet each (24883.2
Greek miles is equal to 24741.8181818 British Standard miles of 5280-feet
each... 24741 & 9/11ths-miles). This was the "6 & 7" combined
number families' way of configuring the Earth for grid referencing and navigation
across the vast oceans.
- The circumference of the stone sphere equates to 114.545454-inches (114
& 6/11ths). The in-built tutorial for the student of navigation relates
to calculating values related to 1-minute of arc and applying the number derived
to higher and lesser expressions of the Earth's circumference. Therefore:
24741 & 9/11ths -miles ÷ 360 = 1-degree of arc ÷ 60 = 1-minute
of arc or 1.14545454-miles or 6048-feet. In this case, the circumference is
114 & 9/11ths inches and substituting inches for miles would mean 100-minutes
of arc or 604800 feet.
- If the Great Pyramid was elongated by a mere 3-inches, then another navigational
system based upon the number family "11" would come into play. This
is the system incorporating a League (16500-feet), Mile (5280-feet), Furlong
or Furrowlong (660-feet), Chain (66-feet), Rod or Perch (16.5-feet), Fathom
(originally 5.5-feet) and Link (7.92-inches). Under this system two circumnavigations
of the Great Pyramid = 6050-feet for 1-minute of equatorial arc, equating
to a full circumference of 24750-miles. This is the system which survived
in Britain and other European countries until the forced, recent imposition
of metrification.
- Under this second reading of Stone Sphere A, it's circumference
would be viewed as 114.5833333-inches (114 & 7/12ths). This is an increase
on the first reading of about .0378 of an inch (about 1/27th of an inch, which
is almost undetectable). This second tutorial would have been included alongside
the first, substituting inches for miles to indicate 100-minutes of arc as
60500-feet.
There was a third system that gave an exact or true reading of the equatorial
circumference as 24883.2-miles of 5280 feet each. This reading was only 18.8-miles
different to the accepted circumference that we use today (24902-miles). Under
this system the circumference of Stone Sphere A would have
been viewed as 115.2-inches or about .7 of an inch larger than Lothrop's circumference
measurement of 114.5-inches. The evidence would suggest that
Lothrop worked in feet and inches, which, as an American was his natural medium
or standard. It would seem that he has also "rounded"
his measurements to the nearest half inch. He has then converted these values
into metric renditions, resulting in complex-looking or cumbersome metric circumference
readings appearing in his report, such as 2.9083 metres for
this sphere.
STONE SPHERE "B"
Lothrop renders this circumference as 3.5814 metres, which, again is a complex-looking
or cumbersome metric reading, but in feet and inches converts fluidly to 11-feet
& 9-inches (11.75-feet) or 141-inches. This stone sphere contains very important
navigational and lunar tutorials in the interpretation of two close-proximity
circumference readings and associated codes. Lothrop's average is 141.322-inches
- A reading of 140.8-inches would be navigational and the circumference of
the stone would be 1/450th of a mile.
- A reading of 141.75-inches would be a very dynamic lunar code and 141.75-days
would be 4.8 lunar months to an accuracy of less than 5-minutes.
- Under the ancient lunisolar Sabbatical Calendar system, 7.2 lunar years
(2551.5-days) were tracked alongside 7-solar years (2556.75-days). There would
be 18-periods of 141.75-days in the 2551.5-day (7.2 lunar years) lunar count.
- The circumference of 141.75-inches would be 1/240th of the perimeter value
of the Khafre Pyramid and 1/256th of the perimeter value of the Great Pyramid.
- The 141.75-inch circumference, if rendered in feet (11.8125-feet
... 11 & 13/16ths), would be used for mnemonic recall
of lunar intervals. There would be, for example, 2.5-intervals of 11
& 13/16ths -days in a lunar month of 29.53125-days (29
& 17/32nds -days). There would be 30 intervals of 11.18125-days
in a lunar year of 354.375-days. The famous "Aztec
Calendar" stone disk has a diameter of 11.8125-feet.
- In the lunar nutation cycle of 6804-days (the big cycle tracked by ancient
European & Mediterranean cousin nations) there would be 48 intervals of
141.75-days.
STONE SPHERE "C"
With stones C, D & E Lothrop only gives diameter values.
Stone "C" equates to 3.5-feet diameter for a circumference of 11-feet
or 132-inches. The sum of 11-feet would be 1/480th of a mile and 1320-feet would
be 1/4th of a mile.
Another tutorial that would, conceivably, have been associated with this stone
is a circumference read as 131.25-inches, which would have provided a lunar
and navigational code of tremendous importance.
STONE SPHERE "D"
Lothrop measured this diameter to be 3.125-feet (37.5-inches), which is a dynamic
ancient code or incremental value that was very important to navigation. When
this is converted by PI @ 22/7ths to a circumference, the result would be so
close to 9.84375-feet to be visually undetectable. The value is a strong lunar
code and 1/3rd part of a lunar month would be 9.84375-days (9 & 27/32nds).
The circumference equated to 118.125-inches,
which in days would be four lunar months to a tolerance of under four
minutes. The Khafre Pyramid of Egypt was built according to a 3,4,5 triangle
method (used by builders and structural engineers since time immemorial), based
upon an increment of 118.125-feet. Therefore, half its base length is 354.375-feet
(118.125 X 3 ... note: a lunar
year is 354.375-days); Its vertical height is 472.5-feet (118.125-feet X 4)
and its diagonal face length is 59.0625-feet (118.125-feet X 5).
The circumference code built into this stone sphere offered up a mathematical
progression from which all of the lunar cycle information could be calculated
by simple ratio. The lunar month was 1/4th of 118.125. The lunar year was 3
X 118.125. The 2551.5-day count for the lunar period within the lunisor Sabbatical
calendar was 118.125 X 21.6 and the 6804-day lunar nutation cycle was 118.125
X 57.6.

The so-called Aztec Calendar or Sunstone, dug up on December
17th 1760 in Mexico City during renovations to a cathedral. It has an official
diameter of 3.60 metres, which measurement is stated in scientific publications
like National Geopgraphic Magazine. The sum of 3.60 metres equals 11.8125-feet
to a tolerance of about 1/56th of an inch (less than half a milimetre).
The circumference, using PI @ 22/7ths , is 37.125-feet
or 445.5-inches, which is a strong navigational code when viewing the
Earth's equatorial circumference as 24750-miles.
STONE SPHERE "E"
The circumference of this stone sphere complies to 10.8-feet, to a tolerance
of about 1/15th of an inch and this value is a dynamic ancient code, much used
for both navigational and lunar calculations, as well as for the duration of
the Precession of the Equinoxes. The progression goes:
10.8, 21.6 (note: the sun spends 2160-years in each house of the zodiac during
the Precession of the Equinoxes), 32.4, 43.2, 54, 68.4, 75.6 (note: the Great
Pyramid is 756-feet long), 86.4, 97.2, 108, 118.8, 129.6 (note: half the period
of the Precession of the Equinoxes is 12960-years), etc.
Continue


