RING O' BRODGAR, ORKNEY ISLANDS
GATEWAY TO THE AMERICAS.

The advanced mathematical principles, found encoded into precisely positioned, purpose-built surveying markers around Ring o' Brodgar and the greater Orkney Islands, tell us the following facts with indisputable clarity:

By about 3000 BC the cousin Caucasoid nations living around the Mediterranean and throughout Continental Europe, were making ocean traversals to the Americas in their very seaworthy, large, planked sailing ships. For this otherwise dangerous undertaking they used Britain as a main staging area and had established several expansive open-air universities for teaching mathematical principles of navigation and cyclic astronomy. In the British Isles great sprawling schools, offering intensive-comprehensive courses, were laboriously built at Avebury Henge and Durrington Walls Henge in Wiltshire, England, as elsewhere.

This European preoccupation with exploration would go a long way towards explaining why such a high percentage of the Algonquain Indian language of North America, extending to the Great Lakes region and almost across the entire continent, contains many clearly identifiable ancient Basque words (the same word used for elbow, foot, head, breast, shoulder, guts, lake, river, louse, birch bark, ocean, boat, snow (falling), snow (on ground)" etc.). Moreover, it's a very ancient form of the Basque tongue, uninfluenced by Indo-Aryan admixtures that crept into the Basque language at later epochs.

Added to that is the fact that the oldest skeletons or mummified remains found across the length and breadth of the Americas are those of Europeans. Also, ancient European structures, cultural-symbolism and writing are found in profusion up and down the Eastern seaboard of the United States, with Hebrew, Phoenician, runic or ogham scripts, etc., seen as far inland as Minnesota, Oklahoma, Ohio, New Mexico, etc. Caucasoid remains are found in Nevada, extending to the Windover bog of Florida or from Mexico to Peru (the Cloud People) & Bolivia, etc. A very high percentage North American Indians carry the European "Y" chromosome and many tribes in both North and South America have oral traditions of the white tribes that their ancestors vanquished. The same measurement & angle standards employed to build ancient Mediterranean-European structures were used to build the huge geometric earthmound complexes of Ohio and Pennsylvania, as well as the temple structures of South America.
http://www.faculty.ucr.edu/~legneref/bronze/bronze4.htm
http://www.philipcoppens.com/copper.html
http://planetvermont.com/pvq/v9n2/megaliths.html

An above article states: 'Puzzlingly, however, carbon dating and archeo-astronomical data at the Mystery Hill [New Hampshire, USA] site reveals a probable start date for the construction there as long ago as 2000 to 2500 B.C. This coincides more closely to the culture that built the great megalithic sites found at Stonehenge and Avebury in England and the immense Ring of Brodgar in Scotland (3000 B.C.).'

Archaeologists working at the Wadi Gawasis caves site of Egypt examine the substantial ship timbers of disassembled, large, ocean-going vessels, which date to as early as 2600 BC. The timbers of these ships were severely infested with marine mollusks (shipworms) and the cave-system at Wadi Gawais was used as a repair facility and storage location for ship-related paraphernalia. Great bundles of rigging ropes, which were still in fine condition despite the 4500-years or so since their manufacture, were found in the dry, sterile caves. These ships, in fleets, had been used to transport goods back though the Red Sea from the far-off land of Punt, located somewhere in the vast, southern reaches of Africa. (Photos courtesy of Florida State University - Boston University & Naples University, 2005).

The most grueling school, however, offering advanced, hands-on experience in battling the stormy North Sea's adverse conditions, was established in the Orkney and Shetland Islands. Here, at this hard-slog "boot-camp", student navigators had to toughen up considerably, get-smart-quick or die, and anyone issuing as a graduate from this great school was as prepared as one could ever expect to be to face the all-too-often adverse conditions and fury of the open-sea.

The main centre for beginners, where rudimentary mathematical principles of navigation were introduced to initiates, was at Ring o' Brodgar, adjacent to Scapa Flow in the Orkney Islands. At the completion of basic tutorials there, student navigators in small groups of up to 7 individuals were assigned various quests to venture out across the landscape of Mainland Island on multiple overland-navigation assignments. The several individual groups were assigned completely different circuitous routes out-and-about then back to the point of departure. This exercise, which would endure over several days or weeks for any circuit, is comparable to modern-day orienteering and was designed to hone navigational skills, with the students walking overland between chambered mounds & cairns to lakeside & seaside sites (later to become brochs) all around and over the island. Anyone sent to this school to receive an education for the benefit of, and sponsored by, their home country, was, undoubtedly, patently unfamiliar with the region and had to constantly take accurate fixes on landmarks like Ward Hill and Cuilags on Hoy Island or Wideford Hill at Mainland's ENE, to stay on the prescribed course.

Poor navigation had its own undesirable set of consequences, which could mean a very uncomfortable night out in the cold (rather than inside a chambered cairn, mound or broch) and a severe tongue-lashing from a resident tutor when the group arrived late, tired and hungry, at their objective. Because the school required considerable outside contributions from many countries to keep it running, ongoing lack-lustre performance by the students would have been curtailed with appropriate severity. The confederation of cousin Caucasoid nations had sent their brightest and best to the school and each student was a representative of his nation. Goof-balls, foot-dragging-slackers, clowns and dunces had no place here. Gaining a sound education in principles in trans-oceanic navigation constituted a very serious business, as graduates of this school would someday be entrusted with the expensive ships, precious cargos and the lives of crewman & stock for their nations. To be a navigator on a ship carried with it tremendous responsibility and prestige within the national consciousness, as well as life-long material rewards.

As students of the Orkney Island's school gained in competence, they could use the many lochs (lakes) to learn on-the-water sailing. The lochs were considerably more passive than the open sea and an excellent beginner's environment for learning practical sailing skills. When one had gained sufficient proficiency, the sailing and subsequent task of navigating accurately to pre-assigned locations could move to the saltwater harbours and channels between the many Orkney islands. Here the swells and currents offered yet another dimension or challenge in the art of sailing, where tacking away from dangerous shoals or struggling against rips required constant mental & physical effort to overcome nature's forces.

Some marker-mound and standing stone objectives arrived at offered no shelter for the night and the students had to either camp out in the open or press on to pre-assigned lodging at a chambered cairn to receive, food, warmth and a comfortable night's sleep out of the elements. Each mound, cairn, broch, standing stone, ring or pond barrow structure, etc., encountered had been very precisely placed on the landscape at a measured distance and coded angle out from the centre of Ring o' Brodgar. The chambered cairns, mounds and brochs themselves provided internal dormitory stalls, where the ever-transient student groups could bed down in their own dry and warm space. A central gallery within these "underworld" chambers sometimes afforded seating benches around a fire, where mathematical lessons, related to that particular structure's coded position, would be taught by the resident Master of the Craft and discussed in depth by the students. Each structure set-out across the landscape was its own classroom and, in consideration of its precise position, the repository of very specialised, factorable numbers related to navigation or cyclic astronomy. All of these numbers, how to generate, manipulate and use them, had to be memorised by rote, repetition as well as constant, ongoing practice by the students.

Unstan (Onstan) chambered cairn, Mainland, Orkney Islands, is reasonably typical of the hundreds of hostel or dormitory dwellings that exist across the Orkney Islands' landscape. These well-insulated "underworld" buildings contained inner stalls, where students could sleep in individualised spaces. The exact landscape positions of these chambered cairns, mounds or brochs was not haphazard, but each building was purpose-placed to sit at an exact distance and angle out from a hub position. In the case of structures on Mainland Island, the hub position was the centre of Ring o'Brodgar. For outlying islands beyond Mainland, each had its own hub position for the island. All of these dwellings, as well as ordinary mounds or standing stone markers, was a classroom in its own right and each contained very significant scientific information that was essential for students of navigation to learn, memorise and apply.

Very similar souterrain structures or chambered cairns, standing stone circles, etc., along with thousands of ancient incised stones with readable European-Mediterranean scripts, are found on the Eastern Seaboard of the United States and date from the 3rd millennium BC. Unfortunately, political-correctness and racial sensitivity rules of engagement don't allow our academics to acknowledge this "in-plain-sight" evidence and it is muted or outrightly suppressed.

TRIANGULATIONS

On Mainland Island each of the sites was very carefully situated to relate, by code-bearing distances and angles, back to the centre of Ring o' Brodgar. The more major sites, however, were carefully positioned to share surveying relationships between each other as North-South or East-West outer markers. In some cases this meant that student navigators could arrive at a chambered cairn (like Unstan) or ring (like Bookan) and view another structure across the landscape, the position of which would provide a perfect orientation onto one of the four points of the compass. From this fix point, manual theodolites (alidade sighting rules) could be precisely orientated to fix onto any other targets around the horizon for readings of their angles off North.

The larger outer structures were also positioned to provide coded distance tutorials between each other, to aid the student in learning all aspects and variations in measurement increments required for navigating on land or at sea. In the case of larger sites like Unstan chambered cairn it could, by virtue of its position and dimensions, provide several varied tutorials simultaneously. Here are examples:

Tutorial one at Unstan ... navigating by the "6&7" mile of 5250'.

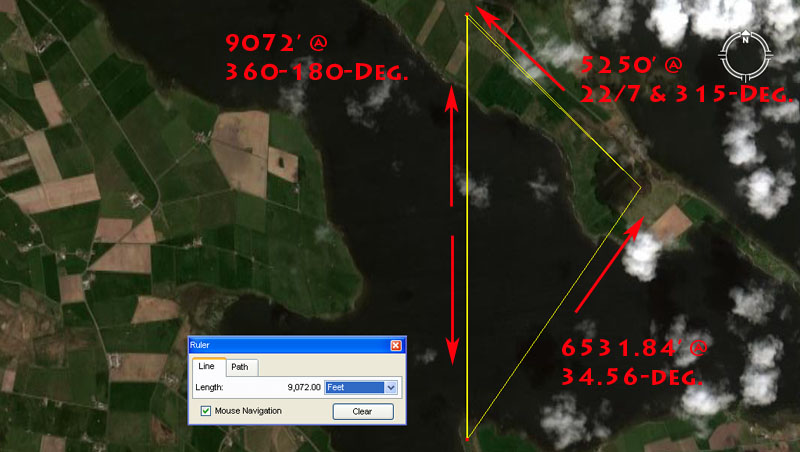
1. The distance from Unstan chambered cairn to the Ring o' Bookan is 9072' @ 360-degrees (true North).

The sum of 9072' is 1.5-minutes of equatorial arc in a world configured to be 24883.2-Greek miles in circumference.

2. The distance from Unstan chambered cairn to Ring o' Brodgar's centre is read as 6531.86' @ 34.56-degrees under this tutorial.

The sum of 653184' would equate to ¹/200th of the 24883.2 Greek mile equatorial circumference.

The 34.56-degree value is navigational coding and the sum of 345.6-miles would equate to ¹/72nd of the Earth's 24883.2-mile circumference.

3. The distance from Ring o' Brodgar to the Ring o' Bookan is 5250' @ a PI angle of (²²/7ths X 100). In keeping with the "6&7" families of numbers the angle could also be read as 315-degrees.

The distance reading is 1 Greek mile and the angle readings are enlarged, mnemonic renditions of PI.

Tutorial 2 at Unstan ... navigating by the "11" mile of 5280'.

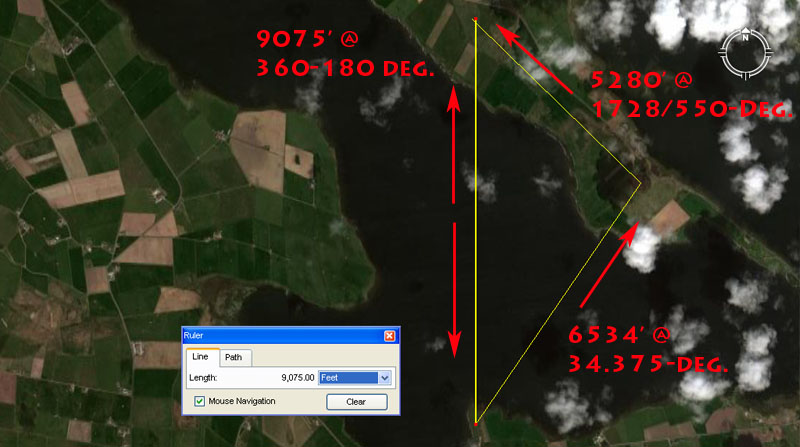
This triangle runs at coded distances and angles between Ring o' Brodgar, the Ring o' Bookan and Unstan chambered cairn. Because of the oval width aspects in the Ring o' Bookan, (seemingly coded to be 146.6666' X 126') or the coded, 90-degrees opposed, diameters of Unstan chambered cairn (seemingly 61.804' X 60.48') there was the built-in opportunity to offer several subtley different tutorials at the same time, as slightly different length and angle vectors would still resolve within the confines of the satellite structures that sat away from Ring o' Brodgar's centre:

1. The distance from Unstan chambered cairn to the Ring o' Bookan is 9075' @ 360-degrees (true North).

The sum of 9075' is 1.5-minutes of arc in a world configured to be 24750-miles (of 5280') in circumference.

2. The distance from Unstan chambered cairn to Ring o' Brodgar's centre is read as 6534' @ 34.375-degrees.

The sum of 653400' is ¹/200th of the 24750-mile equatorial circumference.

The sum of 34.375-miles is half of 1-degree of the Earth's equatorial arc under the 24750-mile reading.

3. The distance from Ring o' Brodgar to the Ring o' Bookan is 5280' @ a PI angle of ¹⁷²⁸/550ths (X 100).

The reading is, of course 1 English mile and the angle divulges the form of PI used to turn such a linear distance (diameter) into a circumference.

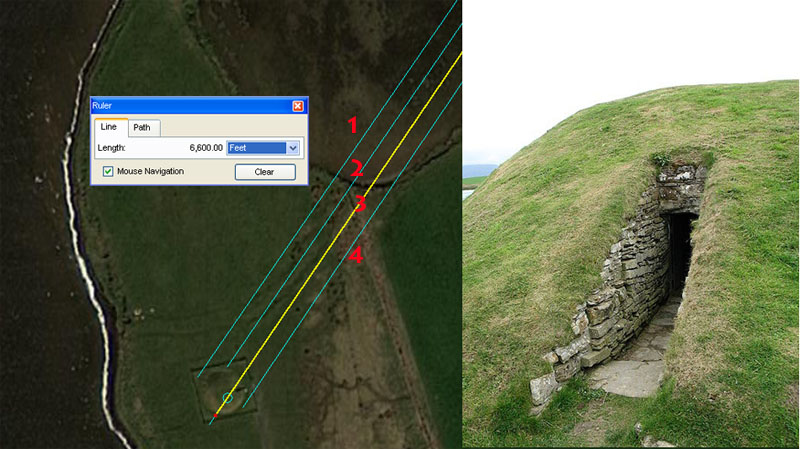
Unstan chambered cairn is seen to be bracketed between a series of coded vectors converging upon it from the centre of Ring o' Brodgar. It becomes obvious that Unstan's precise position and overall dimensions were premeditated to capture several navigational codes simultaneously, with vectors resolving to its face, sides, centre or rear. Two much-used navigational methods, each associated with a different number family, were taught relative to Unstan Cairn's position. One length from Ring o' Brodgar's centre to the approximate centre of Unstan was 6600' or 10 furlongs (furrowlongs) and this incremental value from the "11" family of numbers survived into modern times and is still used.

UNSTAN CHAMBERED CAIRN'S DUE WEST AND EQUINOX, OUTER MARKER STONE.

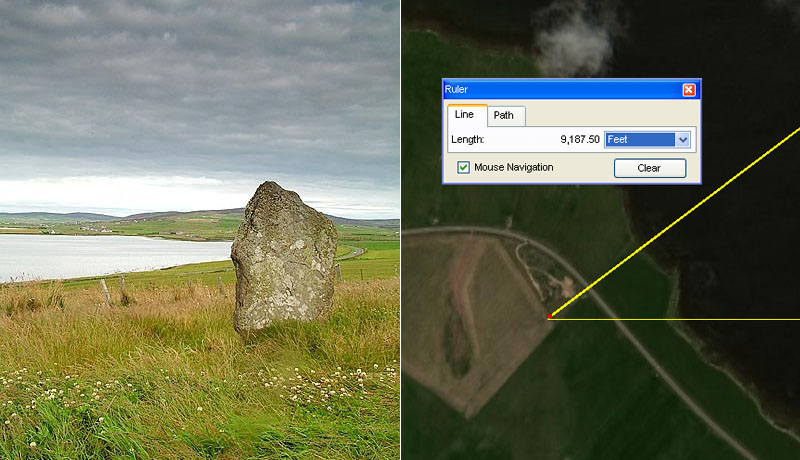
Sitting just slightly south of due West from Unstan chambered cairn's centre is the very large and visible Deepdale Stone, which stands full face towards Unstan cairn. It also sits 1.75 Greek miles from the centre of Ring o' Brodgar at a return azimuth angle of 53.130-degrees. This degree angle is the hypotenuse angle found in all 3,4,5 triangles and one could, therefore, reasonably expect that an ancient marker stone once stood at Cloustan, due South of Ring o' Brodgar @ a distance of 5512.5' (1.05 Greek miles) from Brodgar. The distance due East from the face of the Deepdale Stone to that marker would have been 7350' (1.4 Greek miles) ... if, indeed, the designers of the Brodgar open-air university placed the 3,4,5 triangle (coded in length and angles on all sides) into the landscape.

Such a triangle would have provided dynamic "surveyor's baselines" for triangulation onto targets much further afield.

A line running due East from the Deepdale Stone skims past the southern side of Unstan chambered cairn. The actual, coded degree angle from the Deepdale stone to the epicentre of Unstan cairn is 88.59375 -degrees (88¹⁹/32nds) and there are 88.59375-days in 3 lunar months. The distance from Deepdale stone to the centre of Unstan cairn is 364.5' and, in the ancient lunisolar Sabbatical Calendar count the sum of 364.5-days would constitute ¹/7th part of the 2551.5-days (7.2 lunar years) being monitored alongside 7-solar years (2556.75-days).

Given this slightly South of West and more elevated position of the Deepdale Stone from the epicentre of Unstan chambered cairn, it should have functioned very well as the Equinox sunset outer marker, with the observer watching from the centre of Unstan. Similarly, the Winter Solstice sunset could be observed to occur in the "V" between Ward Hill and Cuilags on the Island of Hoy, when viewed from Unstan.

SO, WHAT SCIENTIFIC INFORMATION WAS BEING TAUGHT AND EXPANDED UPON AT THE RING O' BRODGAR.

• The solar year can be called 365¹/4-days, which is a nice rounded number equating to 8766 hours.
• The lunar year can be called 354³/ 8-days, which is 8505 hours.
• If a calendar is produced that runs for 7 solar years, then that equates to 2556 ³/4-days.
• If the lunar period within that calendar runs for 7¹/5 lunar years (one tenth of 72-years), then that equates to 2551 ¹/2-days.
• If a measurement rule is produced, based upon 5¹/4 feet, then 487 X 5¹/4 = 2556³/4 feet/ days.
• The same measurement rule can be used for the moon and 486 X 5¹/4 = 2551¹/2 feet/ days.
• If an auspicious mistletoe culling ceremony is performed on the 6th day after the calendar commences at the Summer Solstice, then the solar and lunar cycles can end on the same day 7 solar years later.
• If the world is described as 12 X 12 X 12 X 12 X 1¹/5-miles (note: 1¹/5 is a tenth of 12), then that's 24883¹/5-miles...only 18.8 miles short of the true equatorial circumference.
• If one wishes to navigate using a "6&7" series of numbers, those miles can be 5250' each.
• If one wishes to navigate using an "11" series of numbers, those miles can be 5280' each (for a world with a circumference of 24750-miles).

Continue.