1. It was: adjacent 105.6-feet (1/50th of a mile of 5280-feet), opposite 140.8-feet (note: the degree angle from the obelisk at Avebury Henge to the centre ring of the Sanctuary Circle was 140.8-degrees), hypotenuse 176-feet (1/30th of a mile).
2. It was: adjacent 105-feet (1/50th of a mile of 5250-feet ...also 10 Hebrew Reeds), opposite 140-feet and hypotenuse 175-feet (1/30th of a mile of 5250-feet).

It's also very significant that the line running from the centre of Silbury Hill, crossing the crown of "Silbaby" mound and resolving to the centre hubstone of the Sanctuary Circle lies at 105.6-degrees azimuth. The adjacent of the Sanctuary Circle 3,4,5 calculation triangle, lies on an angle of 105.6-degrees from the hubstone.

An Internet photo of the Sanctuary Circle. The 3,4,5 triangle is marked within the Sanctuary with the intersection between the opposite and hypotenuse being a stone situated at the roadside gateway into the site. Photo courtesy of JJ Evendon from the Megalithic Portal website.

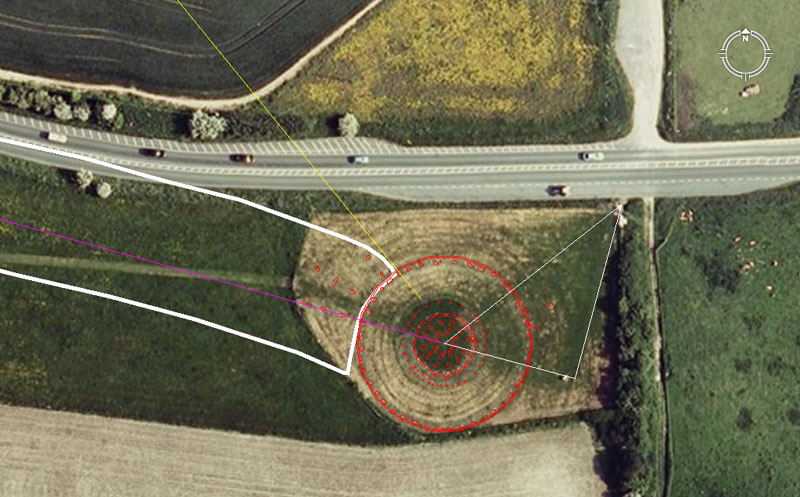
The fine white-line 3,4,5 triangle shown within the Sanctuary is marked by components on the ground. The purple line shown crosses the crown of "Silbaby" mound hill before resolving on the centre of Silbury Hill. The azimuth angle from Sibury Hill is 105.6-degrees. The yellow line extends for 7920-feet (coding the diameter of the Earth in miles of 5280-feet) from the obelisk at Avebury Henge into the Sanctuary Circle. The azimuth angle of the yellow-line is 140.8-degrees from the obelisk (a fraction expression of the mile of 5280). It is seen to brush the bold white lines of the English Heritage drawing that depicts the Avenue terminating at the Sanctuary Circle. In one of two ways of reading the above 3,4,5 calculation triangle at the Sanctuary, the opposite is 140.8-feet ... the same value as that used in the design angle from Avebury Henge obelisk.

This area of the Sanctuary appears to have been dedicated to teaching the 3,4,5 triangle geometric principle. Provision was obviously made for accommodating several sizes of 3,4,5 triangles, ranging from adjacent's that were as little as 96-feet, up to 105.6 and probably 108-feet or more

.

Here's the stone at the Sanctuary gate, which formerly marked the apex of the giant 3,4,5 triangle. Photo courtesy of Hamish from The Megalithic Portal website.

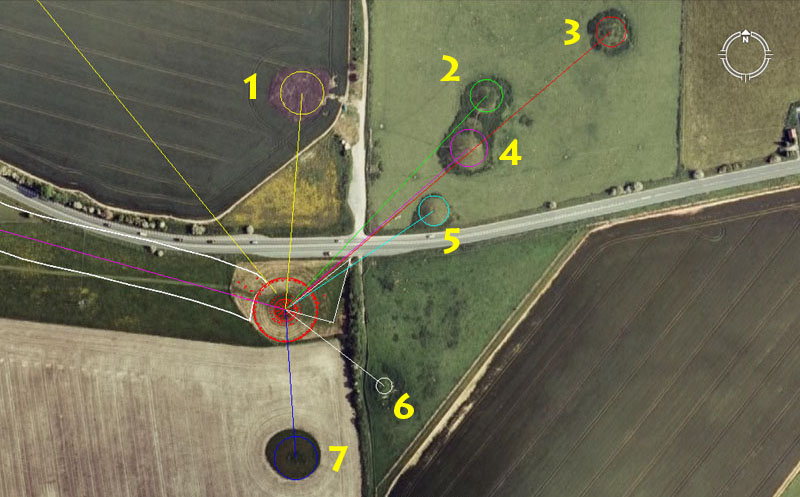
The Sanctuary Circle, situated at the end of the long West Kennet Avenue, was a site of intensive training in triangulation geometry. A series of mounds were built around the Sanctuary, some of which are shown above. Student navigators, working from the hubstone of the Sanctuary calculation circle could take fixes onto the epicentre summits of surrounding mounds or upon markers sitting at various positions on the mounds. Alternatively, students could work from sighting pits and markers on the mounds themselves. The outer mound codes of distance and angle away from the Sanctuary hubstone are:

1. The distance appears to be coding the navigational value, 460.8-feet and the azimuth angle appears to have been 4.4-degrees.
   
2. The distance appears to code the Earth equatorial value, 622.08-feet. In the 24883.2-mile circumference, the sum of 622.08-miles would be 1/40th. The angle is 32.4-degrees, which is also navigational coding.
   
3. The distance appears to be positively coding 907.2-feet, which is navigational. The Great Pyramid is 9072-inches long and 907.2-feet would represent 1/400th of 1-degree of arc under that geodetic assignment. The angle to this mound from the Sanctuary hubstone is 49.5-degrees, which is also navigational coding.
   
4. The distance appears to be coding 518.4-feet and the angle is 48.6-degrees. If one travels 1-league (16500-feet) then this linear distance converts to a circle of 51840-feet using PI @ 3.141818182. The Great Pyramid, which measures 72 Hebrew reeds in length (of 10.5-feet each), covers an area of 5184 square reeds. The sum of 518.4-years would be 1/50th of the duration of the Precession of the Equinoxes, etc., etc. The angle of 48.6-degrees carries a dynamic lunar and navigational value together.
   
5. The distance is positively 378-feet and the small sighting pit depression where this line resolves to is still seemingly in evidence in the Google Earth picture. Half the length of the Great Pyramid is 378-feet or 1/16th of 1-minute of arc. The angle to the pit is 56.25-degrees, which is lunar and navigational coding simultaneously.
   
6. The distance is 262.5-feet, which is a very strong lunar code. The angle also appears to be strongly lunar. The period of 7.2 lunar-years was counted alongside 7-solar years under the Sabbatical Calendar system. The sum of 7.2 lunar years is 2551.5-days. Half that value is 1275.75-days and this angle at the Sanctuary appears to be coded to 127.575-degrees. The distance of 264-feet (1/20th of a mile) would also have been used in conjunction with this little mound's summit.
   
7. The distance is 315-feet (half of a Greek Stadia of 630-feet). This would also have been recognised as 314.16-feet, etc., and the other, close renditions for PI (used in particular calculations) taught in this position. The angle to the centre summit is 176-degrees, which is navigational coding (1/3rd of a mile is 1760-feet).

New Zealand researcher, Barry Taylor squats down in a specially built, ancient sighting pit at Tapapakanga Park, near Thames, NZ to observe the Southern Hemisphere's Winter Solstice sunrise (June 2009) on the distant Coromandel Ranges. From the hilltop sighting pit, which was built by the ancient surveyor-astronomers who occupied New Zealand for thousands of years before the coming of the Polynesian-Maori, the Winter Solstice sun gives a very precise "first glint" fix in a conspicuous "V" trough on the range.

The ancient people built a large beehive house, hovel dome village at Tapapakanga, complete with two large amphitheaters, a stone-lined water course and many mounds or other structures in the sheltered valley by the sea. The late-era Maori warriors attacked them and survivors fled into the seclusion of the rugged Coromandel and Hunua Ranges to hide. The former people were described as "uru-kehu" and "kiri-puwhero" (light, reddish skin complexion, with red or golden tinged hair and other European hues, as well as blue and green eye colouration. They set up similar obelisk, cairn and mound marker systems, using the same measurement and angle standards as one finds in Britain, Continental Europe, the Mediterranean Basin the Americas and Easter Island, etc. Under New Zealand's very politically-correct regime these people are no longer allowed to be acknowledged or remembered, although Maori oral traditions and our earliest history books are replete with references to them. The navigational mathematics of these ancient people is encoded into the New Zealand landscape by marker systems, in exactly the same way as at Avebury. Their positional plotting systems were so sophisticated that they could navigate with relative safety from Europe and the Mediterranean to the "distant isles at the far ends of the Earth" over 5,000-years ago.

Down in the valley where the remains of the village structures are found, Barry stands on a specially built hump that relates to both the Winter Solstice and Equinox sunrises. An arrow is shown ascending from the sighting pit up on the hill where he earlier observed the Winter Solstice sunrise to occur on the distant Coromandel Ranges. From the valley hump position the sun rises from the hilltop pit. In other words, an individual standing in the sighting pit up on the nearby hill became the outer-marker for another observer down at the valley hump to get a precise fix on the Winter Solstice day. The high ranges further afield are often enshrouded in clouds, so this second, somewhat less accurate method offered an alternative Winter Solstice fix.

SETTING SAIL AGAIN DOWN THE WEST KENNET AVENUE

We are now back at the southern gateway of Avebury henge, ready to begin the navigational tutorial encoded into the eastern row. From the big obelisk beside the gate the students would commence their tutorial for either the "11" method of navigation using the mile of 5280-feet (western row) or the "6&7" method using the mile of 5250-feet (eastern row). The giant gateway obelisk represented the beginning point for any journey and the numbered paths shown above to either row mean the following:

1. A line runs for 146.6666-feet to a marker stone. The azimuth angle back to the launch position on the gateway obelisk is 14.66666-degrees. In both distance and angle the coding relates to the 5280-feet mile and 146.66666-feet would be 1/36th of a mile.
   
2. A line runs from position 1 for 110-feet to a stone at the corner of the Avenue. The value 110 is accentuating the "11" series of values found all the way down this row, but the position would also have been used to teach the merits of 112 & 112.5, both of which were very important to either the period of the moon or navigation. The azimuth angle is 340.2-degrees. This coding is lunar in a dynamic sense and 3402-days would be half the duration of the lunar nutation cycle, where the moon moves from lunar major standstill to lunar minor standstill.
   
3. This line has been mentioned already as the start line into the western row. It's 247.5-feet long and on a true North-South.
   
4. This line is also on a true North-South, but runs to a commencement stone for the eastern row. It is 126-feet long or 12 Hebrew reeds, also 120 Greek feet.
   
5. The linking-line coming off the true North-South line towards the eastern row is 84-feet long and runs to 168-degrees. Both of these values are very important to the "6&7" method of navigation (note: 84 X 2 = 168).
   
6. Extending from the gateway obelisk and going directly to the commencement stone for the eastern row is this line of 210-feet length. This length is 120 Celtic or Hebrew Royal Cubits of 21-inches each. The return angle to the gateway obelisk is 354.375-degrees, which once again codes the lunar year of 354.375-days.

As the students start their respective journeys down either row they encounter, what could be considered as, an "out-of-place" lunar code (angle positions for 1 & 6 shown above). The daily position of the moon relative to the Earth and the background of stars that the moon (and sun) rose though and set by, were vital to both navigation and safety at sea. The moon, with its huge gravitational tug on the Earth, the oceans and atmosphere, is the greatest determinant of weather and there are certain seas that one dare not venture into at certain times of the year if the position of the moon is wrong (bad moon). The tutorials relating to the lunar year of 354.375-days and lunar nutation cycle of 6804-days would have been very comprehensive. With a sound knowledge of the lunisolar Sabbatical Calendar, both the sun by day and the moon by night represented major beacons or fix points in navigation, especially in consideration of what house of the zodiac they rose through or set in as the year progressed.

THE TWO SYSTEMS OF LENGTH TO BE FOUND SIDE-BY-SIDE IN THEIR RESPECTIVE ROWS DOWN THE AVENUE

Note: This is a partial list of the main measurements within the standard being described. There were several others within the individual number families and all were in a perfect ratio to their larger grouping. All measurements in both columns are based upon the same "inch", but individual rules could be calibrated to whatever divisions were required for particular types of calculations or trade requirements.

From the partial lists supplied above, or in consideration of other systems such as the so-called "Roman" one with a foot of 11.664-inches and a pace of 58.32-inches, the greater list of related measurements within each known or partially known standard are fully restorable. Each measurement within a system is a factor of or in ratio to all others of the group. Weights, measures and volume standards of the ancient Scottish, Swedish, Germanic tribes or others, including of the more remote cousin nations and forebears who abandonned homelands in the Near East or Northern India, etc., and moved to Europe, will be found to be ratio expressions of the same parcel of integrated, factorable numbers.

We will now consider the eastern row for a total of 32 legs. Using this very versatile system, both a reading of the equatorial circumference for navigation and a reading of the lunar cycle durations for the lunisolar calendar were possible within the same number sets (based upon 5.25).

Leg 1.

The distance is 210-feet and the azimuth angle back to the gateway obelisk is 354.375-degrees.

The sum of 210-feet X PI @ 22/7ths (3.14285714) = 660-feet or 1 furlong (furrowlong). This would mean that a furlong of circumference equated to 22-inches per degree of arc.

Leg 2.

The distance is 75.6-feet and the azimuth angle is 113.4-degrees.

The length would be 1/10th of the side length of the Great Pyramid and 1/80th of 1-minute of arc for a world that was 24833.2 so-called "Greek" miles (of 5250-feet each) in equatorial circumference. This linear length value X 22/7ths = 237.6-feet circumference or .66 of a foot (7.92-inches or 1-link) per degree of arc.

The angle of 113.4 feet is also navigational coding, as well as lunar. Three side lengths of the Great Pyramid @ 756-feet per side = 2268-feet or 1134-feet X 2. Greek historian Herodotus (5th century B.C.) was told by Egyptian priests that the Great Pyramid was 800-feet long. This would mean use of a foot that was 11.34-inches in length. The width of the Station Stones rectangle at Stonehenge was designed to convey 113.4-feet. The sum of 113.4 X 22/7 = 356.4. A circumference of this value, divided by 360 = .99 of a foot per degree of arc.

Leg 3.

The distance is 80.64-feet and the azimuth angle is 126-degrees.

The length of this leg is navigational coding that relates to the equatorial size of the Earth and 80.64-feet would be 1/75th of 1-minute of arc under the Great Pyramid's literal geodetic assignment of 6048-feet per minute of arc. Alternatively, the position could have also been used to teach the number 80.66666-feet (80 & 2/3rds) and related to the equatorial circumference under the 24750-miles (of 5280-feet) assignment. Nevertheless, all of the codes in this eastern row relate to the "6&7" family of numbers and have to be able to convert to a plotting circle using PI @ 22/7ths. Therefore: 80.64-feet X 3.142857 = 253.44-feet or .704-feet per degree of arc. Note: the sum of 70.4-feet would be 1/75th of a mile.

The angle number delivers up one of the most used values of antiquity. The Hebrew reed (10.5-feet) was 126-inches in length. When a diameter based upon 126 is converted to a circle using PI @ 22/7ths the result is 396. This value was also used copiously, especially to describe the equatorial radius of the Earth (3960-miles).

Leg 4.

The distance is 75.6-feet and the azimuth angle remains 126-degrees.

Leg 5.

The distance remains 75.6-feet but the return angle towards the henge becomes 302.4-degrees.

The Great Pyramid was 3024-feet in length for one circumnavigation of all 4-sides and this distance represented 1/2 of 1-minute of arc. This value, if considered to be a diameter, would convert to a circumference of 950.4 or 2.64 per degree of arc. The sum of 264-feet would be 1/20th of a mile.

It's important to remember that this row on the Avenue was teaching students how to navigate in linear legs based upon the "6&7" (5250-feet mile) system. At the end of each leg traveled the distance covered had to be converted to a plotting circle, using PI @ 22/7ths. The circumference had to be divisible by 360-degrees and all numerical expressions derived were in the "11" family of numbers.

Leg 6.

The distance is 78.75-feet and the angle is 126-degrees.

The length is 75 so-called Greek feet of 12.6-inches each or 7.5 so-called Hebrew reeds of 10.5-feet each (a long time before there were any Greeks or Hebrews). The length is also 1/8th of a Greek Stadia (Stadium) of 630-feet. Incidentally, the 6300 value was very important to the ancient builders of the Octagon geometric earthmound complex of Newark, Ohio, U.S.A. and encoded very clearly into the Newark landscape, along with all of the other measurement values that can be positively identified at Avebury in Southern England.

This value, when converted to a circumference = 247.5-feet or .6875 of a foot (8.25-inches) per degree of arc. Remember that under the Great Pyramid's second geodetic assignment the equatorial circumference was factored to be 24750-miles and 1-degree of arc was 68.75-miles.

Leg 7.

The distance is 82.03125-feet (82 & 1/32nd) or 1/64th of a Greek mile of 5250-feet. When this length is converted to a circle using PI @ 22/7ths it equals 257.8125-feet (257 & 13/16ths). This value equals 150 Egyptian Royal Cubits of 20.625-inches. This was the second of three very closely sized Royal Cubits and it worked with the mile of 5280-feet. A circle of this circumference equates to 8.59375-inches (8 & 19/32nds) per degree of arc. The values derived in a mathematical progression based upon 8.59375 are very important navigational and lunar codes.

The angle is 302.4-degrees.

Leg 8.

The distance is 78.75-feet and the azimuth angle back to the henge is 302.4-degrees.

In the next segment we'll cover 24 more legs on the eastern row, all of which were devoted to teaching the "6&7" method of navigation. Perhaps the very old English saying "today I'm all sixes and sevens" (to be in a state of confusion or disarray) has some root origin in this intensive, ancient training on the West Kennet Avenue. There are other very old variations on the saying, like "to set the world at six and seven" ("to hazard the world" or "to risk one's life"). Certainly, the training on the eastern row of the West Kennet Avenue "set the world at six and seven" and any trainee navigator venturing out to plot a "6&7" course on the often violent open sea was going "to hazard the world" or "risk one's life".

As has been demonstrated, even if one was working their way down the Avenue under the "11" system, the plotting circle created from the linear distance traveled (diameter) was a "6&7" circumference. This intensive navigational training by rote and repetition would have been very mentally taxing and the dunce had no place in this school, which only catered to the the brightest and the best that society could offer (the gifted few set aside to bless the many).

As the Water Rat said to Mole in "Wind In The Willows":

`Believe me, my young friend, there is NOTHING--absolutely nothing--half so much worth doing as simply messing about in boats.

Continue